과소적합(Underfitting)
모델이 너무 단순해서(충분히 복잡하지가 않아서) 데이터의 내재된 구조/패턴을 학습하지 못할 때 발생한다.

머신에게 공을 학습시켜야 한다고 가정해보자. 먼저 축구공, 야구공, 농구공 들의 데이터를 보여주면서 "이런 동그란게 공이야" 라고 가르치게 될 것이다. 이렇게 학습이 될 경우, 테스트 과정에서(새로운 데이터) 사과같이 동근 과일이나 보름달도 공으로 예측할 수 있지만, 학습 때 보여주지 않은 다른 수많은 동근 공(테니스공, 배구공, 골프공 등)들도 어쨌든 동그라니 공으로 맞게 예측하게 되는 것이다.
예측 곡선이 학습데이터를 제대로 학습하지 못해, 패턴을 반영하지도 못하니 훈련 데이터에서도 오차가 크고, 동근 애들은 공이 아닐지라도 공이라 예측해버리니 테스트 데이터에서의 오차도 크게 나온다.
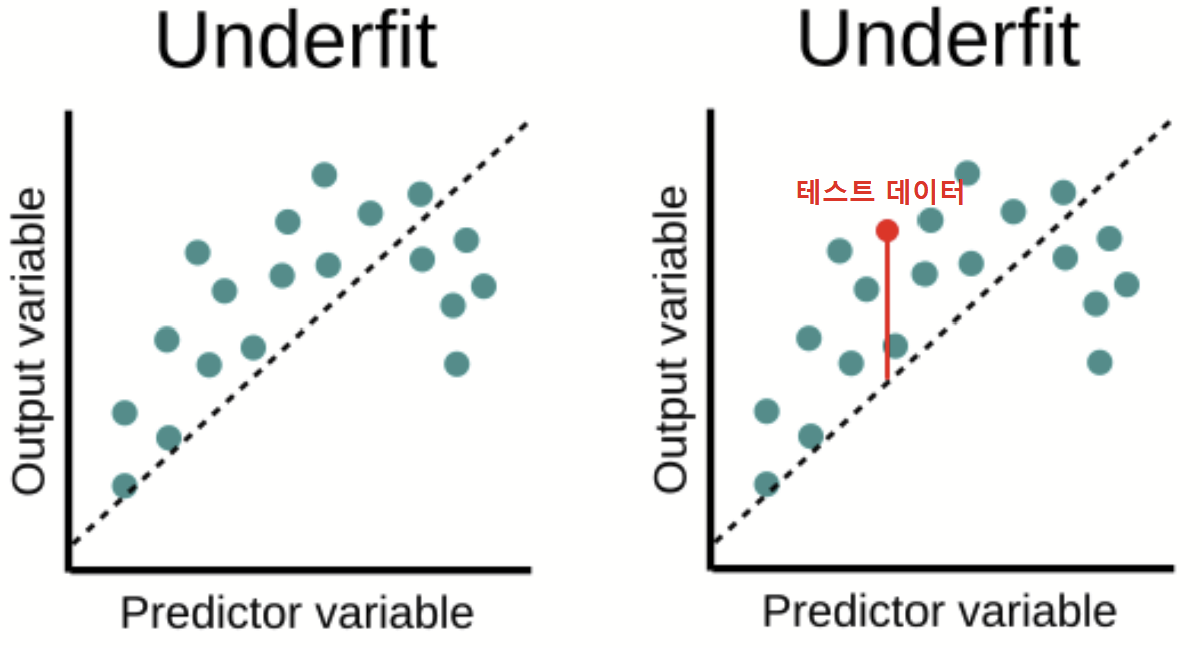
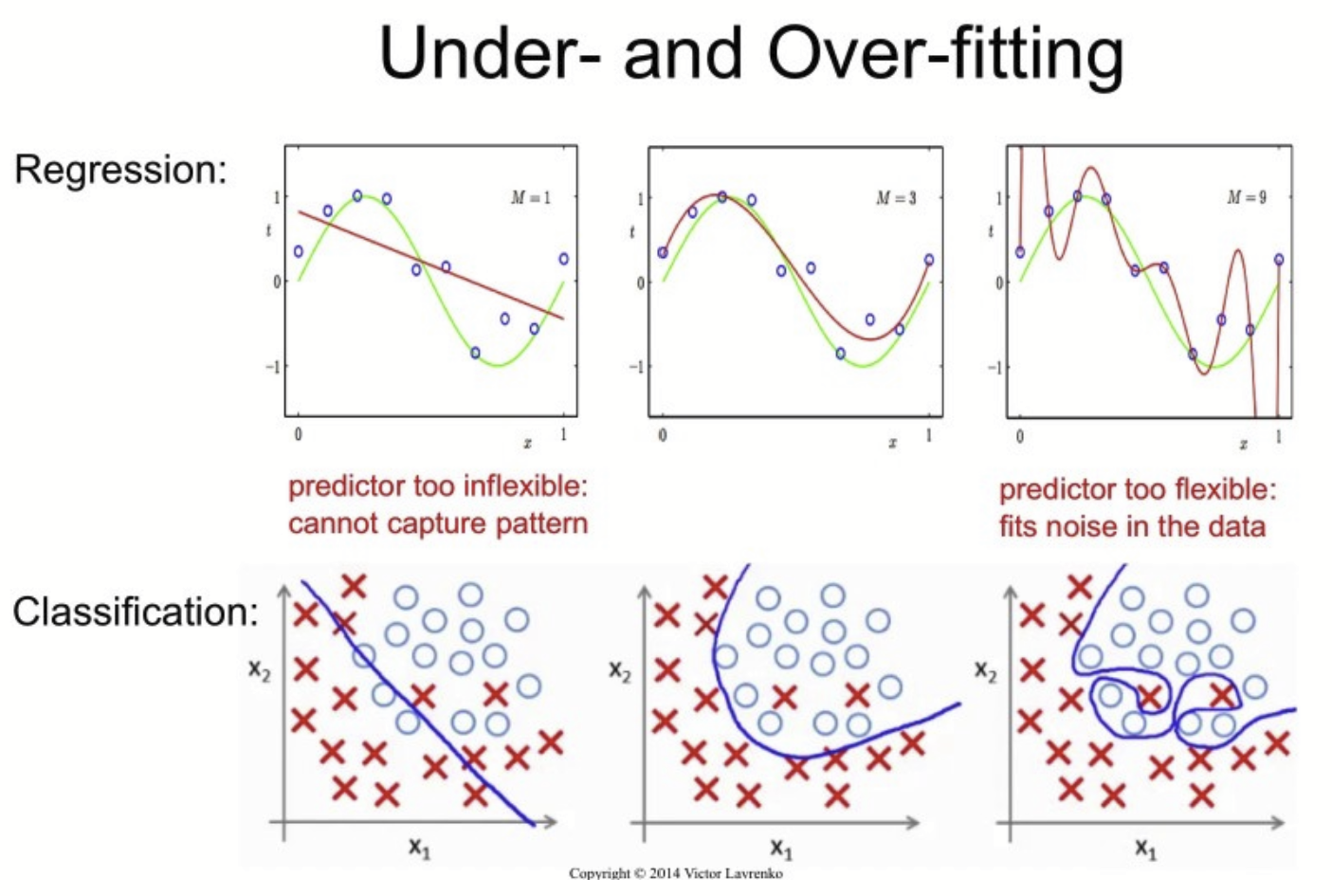
위의 그림처럼 모델이 지나치게 단순하다면 데이터 간의 특성을 구분하기 어려워져서 과소적합(Underfitting)이 발생한다. 학습 데이터셋을 제대로 회귀(Regression)하지 못했으니, 비슷한 테스트 데이터를 비교했을 때에도 큰 오차가 보인다.
과대적합(Overfitting)
과적합은 과소적합의 반대개념으로 생각하면 된다. 모델이 훈련 데이터에만 너무 잘 맞게 학습(지나치게 복잡하게 학습하여)이 이루어져버려서 정작 테스트 환경에서 새로운 데이터에 대한 예측이나 분류를 제대로 수행하지 못하는 것을 말한다.

위에 공 학습 문제에서 공의 다른 특성들(공은 가지고 놀 수 있다, 먹을 수 없다 등)을 추가해 학습을 시킨다면 학습이 잘 된 모델이 될 것이다. 그런데 여기서 욕심을 부려 본질적이지 않고 중요하지 않은 부차적인 특성이(실밥을 가진다, 지름이 7cm 이상이다) 과하게 학습되었다고 해보자. 이 경우 아주 작은 잡음까지 모델이 수용하게 되어 훈련집합은 완벽에 가깝게 대변하게 되지만, 처음 보는 새로운 데이터는 제대로 대처하지 못하게 되는 것이다. (부차적인 특성이 과하게 학습되어 골프공이나 탁구공을 공에서 배제해 버림)
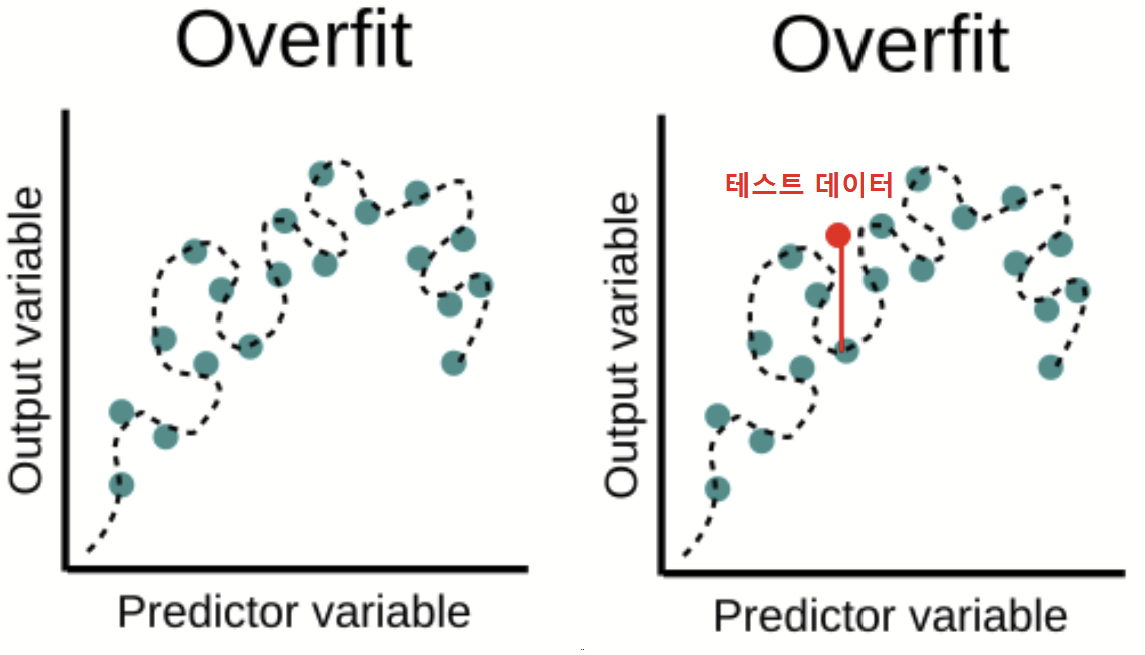
위의 그림에 보이듯, 학습 데이터를 거진 완벽하게 근사했던 모델도 테스트 데이터와 작지 않은 오차를 내는 것을 알 수 있다.
편향(Bias)과 분산(Variance)
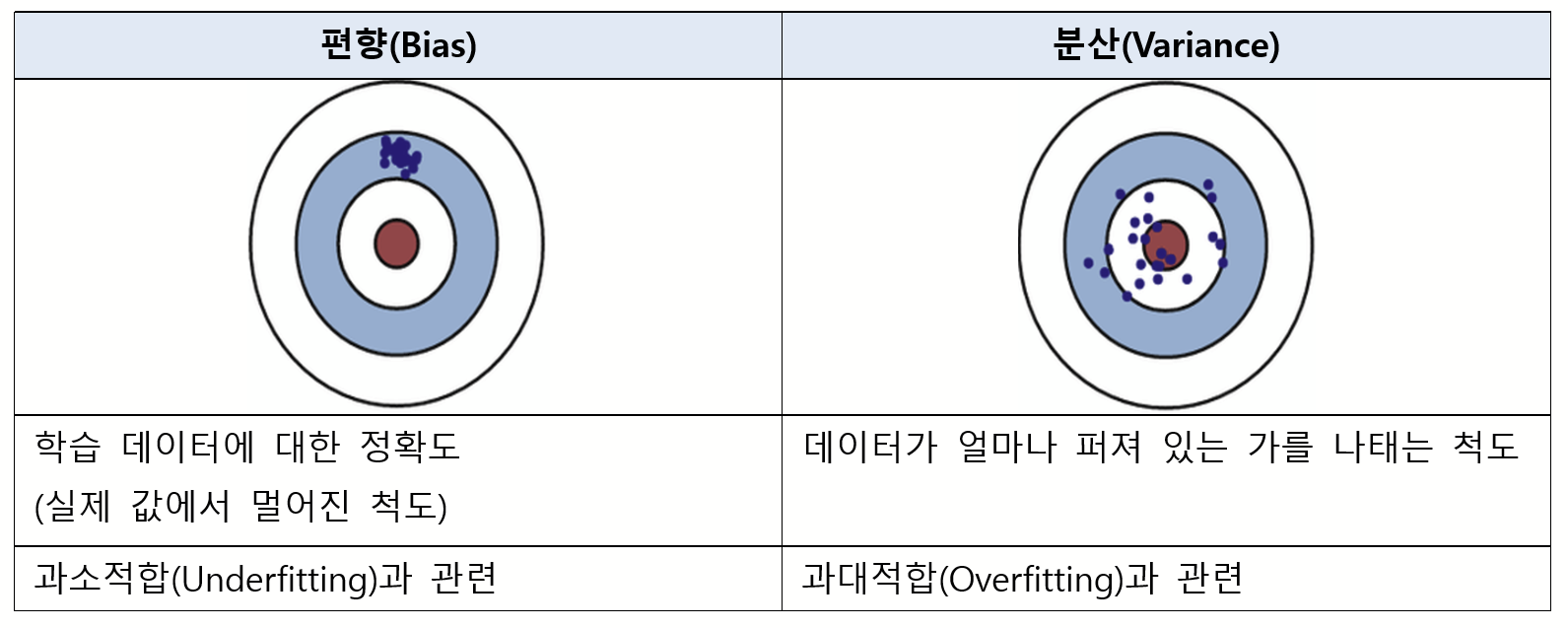
과소적합과 과적합은 오차의 편향(Bias)과 분산(Variance)개념과 관계가 있다. 편향과 분산은 모두 알고리즘이 가지고 있는 에러의 종류로 편향은 학습 데이터에 대한 정확도(실제 값에서 멀어진 척도)라고 이해해 볼 수 있고, 분산은 데이터가 얼마나 퍼져 있는 가를 나태는 척도다.

파란색 점들은 데이터고 과녁의 빨간 부분이 정답지이다. 좌측 상단(Low Bias, Low Variance)은 예측 결과가 실제값과 매우 근접하면서도 예측 변동이 크지 않고 특정 부분에 집중되어 있으니 모델의 성능이 아주 뛰어난 것으로 볼 수 있다. 우측 상단은 예측 결과가 실제값과 근접하기는 하나 넓게 분포되어 있는데, 이렇게 분산값이 높은(high Variance) 경우를 과적합(Overfitting) 상태라 볼 수 있다. (학습해보지 않은 것들에 대한 예측도가 떨어짐) / 이와 반대로 편향값이 높은(high Bias)의 경우 과소적합(Underfitting) 상태라 볼 수 있다. 실제값에는 근접하지도 못하고 특정 부분에만 예측이 집중되어 있으니, 학습 데이터가 제대로 학습되지 못했음을 알 수 있다.
모델의 복잡도(Complexity)
- 선형에서 비선형 모델로 갈수록, 복잡도가 증가한다
- (모델의 파라미터 수가 점점 더 증가함 ⇒ 학습할 수 있는 모델의 파라미터가 많아진 것 ⇒ 데이터에 대한 학습을 더 완벽하게 진행할 수 있음)
모델의 복잡도가 증가하면 할수록, 학습에 대한 정확도도 점점 증가를 하게 된다. 학습의 정확도만 따져봤을 때에는 비선형 모델이 좋으나, 실제 평가 데이터 셋은 학습 데이터 셋과는 좀 다른 분포를 가질 수도 있기 때문에 평가 정확도가 오히려 떨어지는 과적합 문제점이 생기게 된다. 그래서 무작정 파라미터의 수를 늘리는, 복잡도를 증가시키는 이 행위가 꼭 정답만은 아니다.
편향과 분산 트레이드 오프(Bias-Variance Tradeoff)
단순한 모델에서 발생하는 편향을 줄이기 위해 모델의 복잡도를 늘리면 분산이 늘어나고, 복잡한 모델에서 분산을 줄이기 위해서 모델을 단순화 하면 편향이 늘어나게 된다. 편향과 분산은 한쪽을 줄이면 다른 한쪽이 증가하는 성질이 있는데, 이를 편향-분산 트레이드오프(Bias-Variance Tradeoff)라고 한다.

모델의 복잡도가 낮으면 낮을수록, 선형 모델인 경우, 과소적합 현상이 심해서 편향에 대한 에러가 굉장히 큰 상태가 된다. ( 동근게 공이라고 하니, 달과 사과, 단추 등도 전부 공이라고 해버리는 것) 하지만, 비선형 모델로 넘어가면 넘어갈수록, 학습 데이터셋을 더 완벽하게 맞추고 언더피팅 문제가 해소되기 때문에 편향관련 에러가 줄어들게 된다.
선형 모델은 어떤 데이터셋이 여러 번 들어와도 일관된 에러의 크기를 보여주기 때문에 분산에러는 굉장히 작지만, 비선형모델이 되면 될수록 학습데이터셋에 완벽하게 맞춰져버리는 오버피팅 이슈가 발생하기 때문에 실제 다른 데이터셋에 대한 오차는 들쑥날쑥하게 된다. 그래서 위 그래프처럼 분산 관련 에러가 크게 증가하게 된다.
최적의 모델은 저 중가운데 위치하게 된다. 모델의 복잡도나, 어떤 모델을 사용해 학습을 시킬지 또한 하이퍼 파라미터(직접 사람이 정해주는 매개변수)에 속하니, 요런 하이퍼파라미터를 실험을 통해서 결정을 잘 해줘야한다.
오컴의 면도날(Occam's razor)
편향이 큰 모델과 분산이 큰 모델 중 어떤 모델을 선택하는 것이 좋은 걸까? 특정 데이터셋을 통해 학습시킨 결과 전체 오차는 같지만 편향과 분산의 비율이 다른 두 모델이 생성되었다고 해보자. (모델1 ⇒ 편향7: 분산3 / 모델2 ⇒ 편향3 : 분산7) 이 두 모델 중 어떤 모델을 선택해야 할까? 이럴 때는 오컴의 면도날을 생각하면 된다.
“많은 것들을 필요없이 가정해서는 안된다” (Pluralitas non est ponenda sine neccesitate.)
“더 적은 수의 논리로 설명이 가능한 경우, 많은 수의 논리를 세우지 말라.”(Frustra fit per plura quod potest fieri per pauciora.)
- 위키피디아 : 오컴의 면도날 -
이는 쉽게 말하면, “같은 현상을 설명하는 주장들이 있다면 그 중 가장 가정이 적은 것을 선택하라” 라는 의미라고 한다. 따라서, 고려하는 특성이 더 많은 복잡한 모델을 배제해주면 된다. 결론은 좀 더 단순한(간단한) 모델인 편향의 비율이 높은 모델을 선택하는 것이 더 옳다.
오컴의 면도날 결론
"불필요한 가정은 하지 말고 필요한 요소들만 사용하여 학습 데이터를 구성하고 학습을 해야 한다"
해결방법
1. 과소적합 해결방법
1) Parameter가 더 많은 복잡한 모델을 선택한다.
2) 모델의 제약을 줄인다. (규제 하리퍼파라미터의 값 줄이기)
2. 과대적합 해결방법
1) 데이터의 개수를 늘린다.
2) Feature의 개수를 줄인다.
3) Parameter 선정을 적절히 한다.
4) 훈련데이터의 잡음을 줄인다.
5) 검증 데이터 셋을 활용한다. (K-fold cross validation 사용)
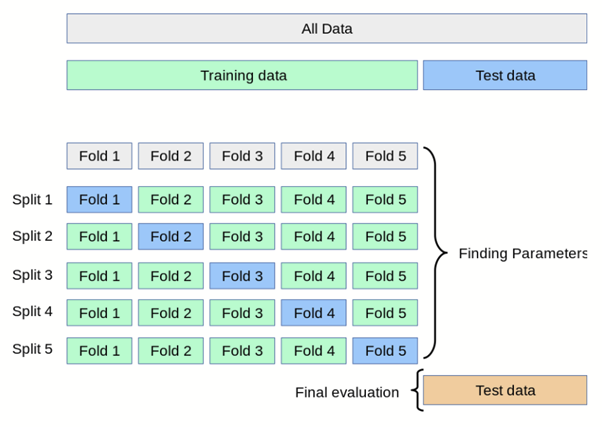
- 일반적으로 사용되는 교차 검증 방법 중 하나로, Training set과 Validation을 여러번 나눈 뒤 모델의 학습을 검증한다.
- 보통 회귀 모델에 사용된다.
- 위 그림에서는 데이터를 K등분(5등분)한 뒤, $1/5$를 검증데이터로 나머지 $4/5$를 학습데이터로 나누다. 각각의 $1/5$를 검증데이터로 바꾸며 성능을 평가한다. 그 결과 총 5개의 성능 결과가 나올 것이고 이 5개의 평균을 학습 모델의 성능이라 판단한다.
- K값이 커진다는 건 학습 데이터 셋이 많아진다는 뜻 ⇒ Bias 에러는 작아지나 Variance 에러는 커진다. K 값이 커진만큼, 더 많은 계산을 돌려야하니 계산비용도 증가한다.
6) 조기 종료(Early Stopping)
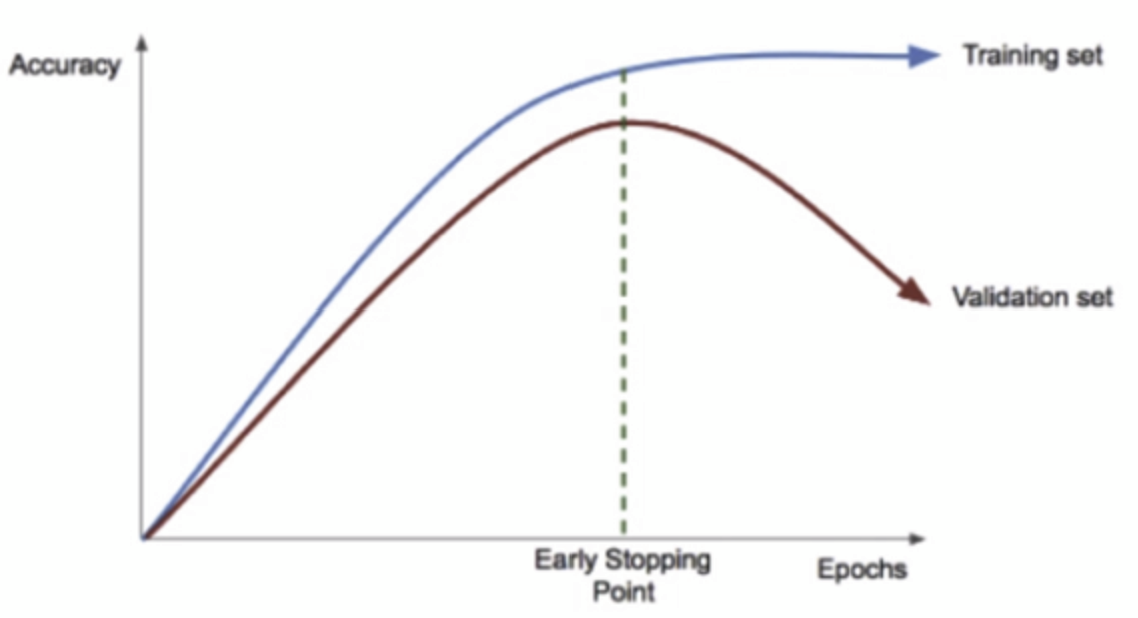
- 딥러닝은 여러 층으로 이루어진 뉴런들을 Epoch 수를 조정하면서 반복해서 계속 학습시키는 것이다. 이렇게 반복이 계속 되다보면 어느 시점에서부터는 학습 데이터셋에 대한 정확도(Accuracy)는 올라가나, 검증 데이터셋(Validation set)의 정확도는 멈추거나 낮아지는 지점이 온다. 이 Validation 의 정확도가 더 이상 올라가지 않을 때, 학습을 멈추는 것을 Early Stopping 이라고 한다.
7) 정칙화(Regularization)를 적용한다
[정칙화 개념]
- 복잡도가 큰 모델을 정의하고, 그 중 중요한 파라미터만 학습하면 안될까?
- 엄청나게 큰 복잡한 모델을 정의해보고 언더피팅 이슈를 없애주는 상황속에서 그 중에서 중요한 파라미터 몇 개만 학습하자
- 필요 없는 파라미터 값을 0으로 만들자!
[정규화 종류]
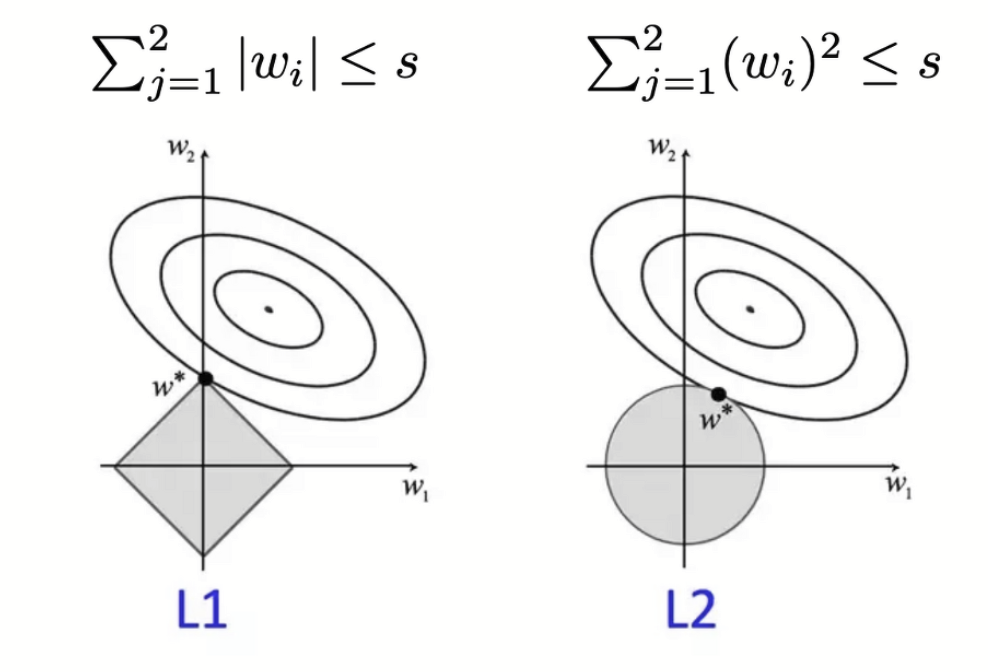
- Ridge 회귀(L2 regression)
- Lasso 회귀(L1 regression)
일반적으로 모델의 복잡도를 키우고, 과적합을 막는 방법론을 사용한다.
요약
참고
https://yngie-c.github.io/machine%20learning/2020/04/30/training_test_reg/
https://bigdaheta.tistory.com/20
https://nittaku.tistory.com/289
https://heytech.tistory.com/125
https://m.blog.naver.com/qbxlvnf11/221324122821
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| Classification: 붓꽃(Iris) 데이터 분석하기 (1) | 2023.04.19 |
|---|---|
| Train data | Test data | Validation data 차이 (0) | 2023.04.19 |
| 배치 사이즈(batch size) | 에포크(epoch) | 반복(iteration) 차이 (2) | 2023.04.18 |
| 손실함수(Loss function) (0) | 2023.04.13 |
| 최적화와 경사하강법(Gradient Descent) (0) | 2023.04.12 |



