풀링(Pooling) ft. Max & Average Pooling

출처: https://kr.mathworks.com/discovery/convolutional-neural-network-matlab.html

 

합성곱 신경망에서 합성곱 연산과 활성화 함수  ReLU로 이루어진 합성곱층 다음에는 보통 풀링층이 존재한다. 풀링층은 각 특징맵에서 독립적으로 작동한다. 풀링은 특징 맵의 높이와 너비를 줄임으로써 특징 맵의 해상도를 낮추지만 분류에 필요한 맵의 특징은 유지시키는데 이를 다운 샘플링(Down-sampling)이라고 한다.

 

풀링층을 사용하는 이유

: 표현의 공간 크기를 점진적으로 줄여 네트워크의 매개변수 및 계산량을 줄이고 과적합을 제어할 수 있다.

 

 

최대 풀링(Max Pooling)

출처: https://developersbreach.com/convolution-neural-network-deep-learning/

 

풀링에서 사용하는 일반적인 방법은 최대값을 추출하는 위와 같은 맥스 풀링이다. 필터와 겹치는 영역안에서 최대값만을 추출한다. 위의 예시는 2 x 2 의 필터로 4 x 4 의 크기를 가진 입력이미지에 스트라이드 = 2를 적용했을 때다.

 

 

평균 풀링(Average Pooling)

 

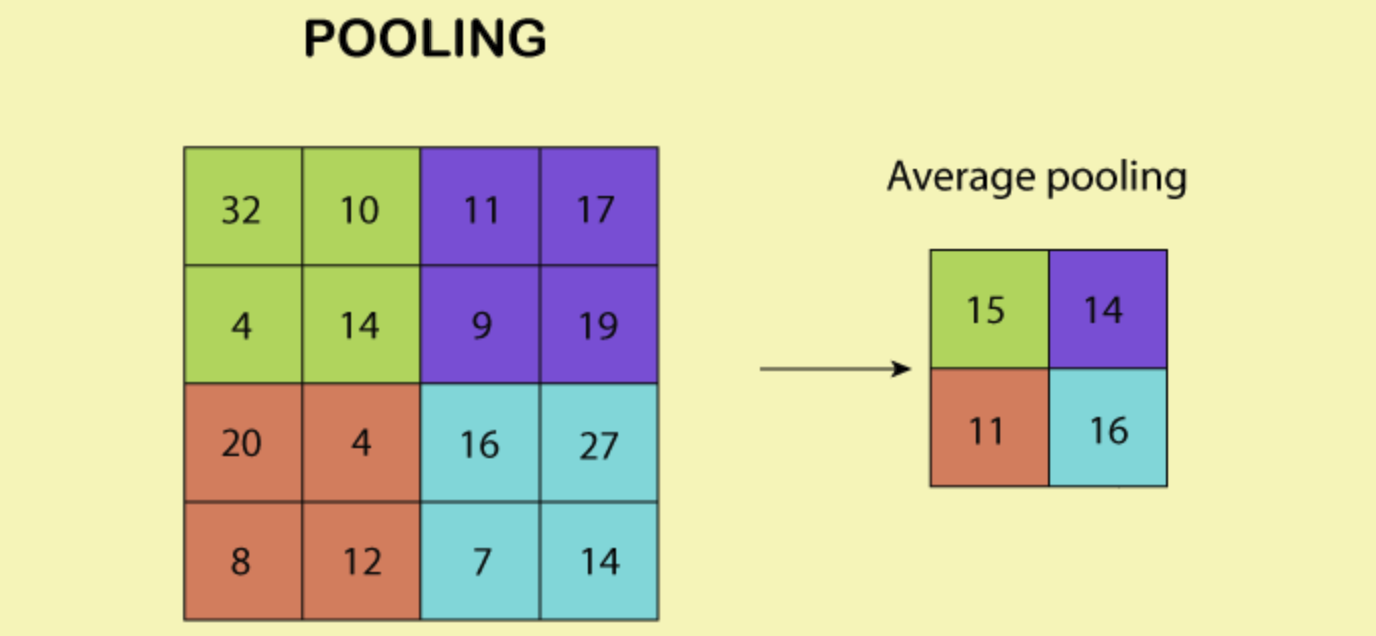
맥스 풀링만큼 자주 사용되지는 않는 풀링의 한 방법이다. 최대값을 취하는 대신 필터와 겹쳐지는 영역의 평균을 취한다.

 

 

 

풀링의 특징

• 필터의 사이즈 f 와 스트라이드의 크기 s, 이렇게 두개의 하이퍼파라미터를 가진다.
• 일반적으로 f = 2, s = 2 를 자주 사용하며 이를 통해 입력으로 들어오는 이미지의 높이와 너비를 절반만큼 줄인다.
• 입력 이미지의 채널과 풀링을 통해 나온 특징 맵의 채널수는 같다.
• 패딩을 사용해도 되기는 하지만 거의 사용하지 않는다.
• 학습할 수 있는 매개변수가 존재하지 않다.
• (➱ 필터안의 수는 입력이미지로부터 뽑아온 수니 별도로 학습되어가며 최적의 수로 찾아지는 매개변수가 아니다.)

 

 

이해를 돕기 위한 예시 / 출처: https://towardsai.net/p/l/introduction-to-pooling-layers-in-cnn

 

 

 

 

정리 및 공부한 내용  참고출처:

https://towardsdatascience.com/covolutional-neural-network-cb0883dd6529

https://developersbreach.com/convolution-neural-network-deep-learning/

https://kr.mathworks.com/discovery/convolutional-neural-network-matlab.html

https://towardsai.net/p/l/introduction-to-pooling-layers-in-cnn