해당 글은 유튜브 채널(https://www.youtube.com/@Deeplearningai) 의 Machine Learning 강의를 정리한 글입니다.
분류 문제를 선형 회귀로 해결할 수 없는 이유
선형 회귀(Linear regression) 문제는 집의 크기와 방의 크기 등의 피쳐값을 통해 집의 가격을 알아보는, 즉 예측값이 연속적인 값으로 나오는 문제들에 대해 사용되었다. 그렇다면 어떤 사진이 고양이인지 아닌지 라던가 환자가 어떤 병을 가진지아닌지 또는 숫자 이미지가 0부터 9까지의 숫자 중 어떤 숫자를 가리키는지 등과 같은 분류 문제는 집의 가격을 예측하는 문제처럼 선형식을 통해 해결할 수 있을까?
환자의 종양의 크기를 보고 이 종양이 악성종양인지 아닌지를 예측해야한다고 해보자.

해당 분류 문제를 Linear regression을 통해서 해결해야 한다고 생각해보면, 그래프는 위와 같이 생길 것이다.
- X로 표기된 훈련 데이터: 악성종양, 클래스1
- O로 표기된 훈련 데이터: 약성종양, 클래스0
훈련 데이터들을 보면, 두 클래스가 각각의 클래스로 몰려있는 형태다. 현재 Linear regression을 사용중인데, 이 경우 예측값이 우리가 원하는 단 두 가지의 클래스인 '0'과 '1'이렇게 두 개의 값만을 가지는 것이 아니라, 0과 1사이에 모든 값을 넘어서, 0이하의 값, 1이상의 값 전부를 예측한다는 뜻이다. 하지만 우리의 목표는 이 데이터가 속한 카테고리를 예측하고 싶은 것이다.
여기서 하나 시도해볼 수 있는 것은, 예로 1과 0사이의 중간인 0.5를 임계점(Threshold)으로 두어, 이 값을 넘을 경우 악성종양인 클래스1로, 넘지 않을 경우 클래스0으로 분류하는 것이다.
[ $f(x) < 0.5$ ➱ $y = 0,f(x) \leq 0.5$ ➱ $y =1$ ]
이렇게 정하구 그래프를 보면, 뭔가 이 데이터 세트에 대해 선형회귀모델이 합리적인 것 같아 보이긴 한다.

하지만 만약에 하나의 훈련 샘플이 저 멀리 떨어진 곳에 추가되었다고 해보자. 그러면 선형 회귀 모델은 초록색 그래프처럼 모습이 변경된다. 이럴 때 임계점으로 잡은 0.5를 기준으로 왼쪽은 클래스 0, 오른쪽은 클래스1 로 나눌 경우, 오류가 생긴다. (두 개의 훈련샘플 x가 클래스 1이 아닌 0에 분류되어 버림, 즉 제대로 분류할 수 없는 모습)
Logistic Regression

Linear regression은 분류 문제와 맞지 않다. 그와 대조적으로 Logistic Regression은 우리의 선형식을 저런식의 모양으로 만들어준다. 이 함수는 시그모이드(Sigmoid) 함수라고 불리며 아웃풋의 값을 항상 0과 1 사이로 가질 수 있게 해준다.
Logistic Regression의 아웃풋이 뜻하는 바

로지스틱 함수의 결과로 나온 값은 이 훈련 데이터 샘플 $x_j$ 가 클래스 1일 확률은 얼마나 될까? 를 의미한다. 예를 들어 로지스틱 함수의 값이 0.7이 나왔다면, 해당 데이터 샘플은 70%의 확률로 클래스1에 속한다는 것이다. 이는 해당 데이터가 클래스 0일 확률은 30%라는 말과 같다. (클래스0에 속할 확률 + 클래스1에 속할 확률 = 1)
결정 경계선 (Decision Boundary)
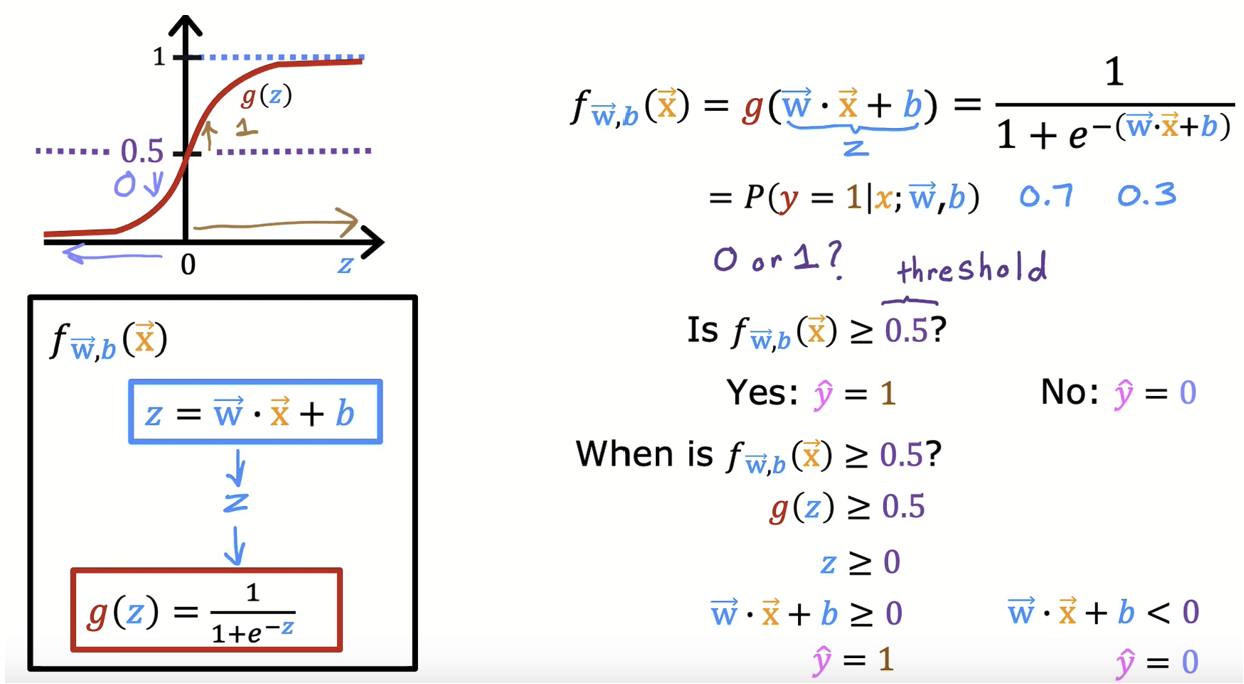
0%와 100%의 중앙값인 50% = 0.5를 임계점으로 두어 훈련 데이터의 카테고리를 나누는 경계선을 만들 수 있다. 시그모이드 그래프의 형태를 통해, 시그모이드 함수값이 0.5 이상인 경우(= 클래스 1에 속하는 경우)는 선형식 z가 0이상인 경우를 얘기하고, 함수값이 그 이하인 경우(= 클래스 0에 속하는 경우)는 z가 0 미만인 경우니, $z(= wx+b) = 0$으로 결정 경계선을 구할 수 있다.


첫 예시처럼 결정 경계선이 선형인 경우도 있지만, 모델식이 얼마나 복잡하냐에 따라서 결정 경계선의 모양은 위와 같이 다양한 형태를 띄기도 한다.
Logistic Regression의 비용함수(Cost function)

Linear regression 문제에서 사용하는 손실 함수는 Squared error cost 다. Linear regression 에서 Squared error cost 를 사용하면, 왼쪽 그래프처럼 비용함수와 매개변수 그래프에서 볼록(convex)함수가 생성되어 경사 하강법을 통해 쉽게 최저점에 도달할 수 있다.
하지만 Logistic regression 의 경우 손실함수로 Squared error cost 를 사용하면, 오른쪽 그래프처럼 수많은 local minimum이 생기게 된다. 이 경우에 경사 하강법을 사용하면 하나의 글로벌 최소점에 도달하지 못하고 지역 최소점에 빠지게 된다.
즉 logistic regression에 Squared error cost 함수는 맞지 않다. 이 non-convex한 부분을 convex 하게 바꿔주어, 경사 하강법에서 쉽게 global minimum에 도달할 수 있게 해주는 비용함수가 존재한다.

Logistic Regression의 비용함수다. 속해 있는 클래스에 따라 식이 다른데, 이 두식을 아래처럼 하나의 식으로 표현할 수 있다. (이 식에 $y^i = 1%$또는 $0$ 을 대입해보면 식이 두 조건에 성립함을 알 수 있음.)
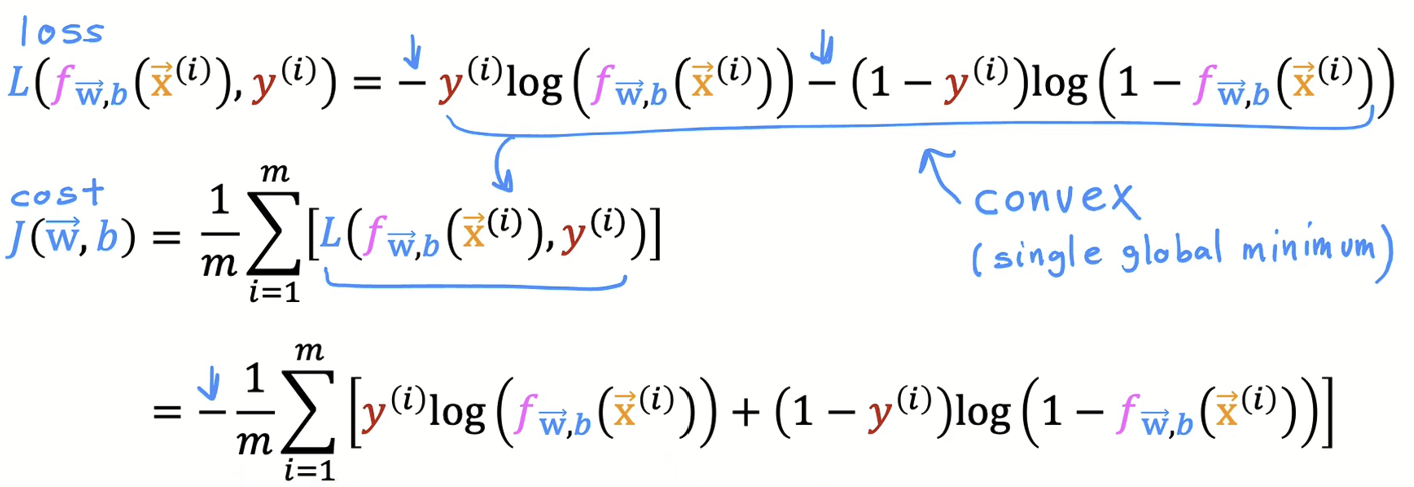
Logistic Regression 의 비용함수는 이렇게 생겼다.
- 손실함수(Loss function) : (i)번째 데이터 샘플의 손실값
- 비용함수(Cost function): 전체 데이터 세트의 손실값의 평균 (m: 전체 데이터 개수)
참고
https://www.youtube.com/@Deeplearningai
사진 출처
https://www.youtube.com/@Deeplearningai
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| 경사하강법의 세 종류(BGD, SGD, MGD) (1) | 2023.05.17 |
|---|---|
| 가중치 규제 (Weight Regularization) ft. 과적합 해결하기 (0) | 2023.05.09 |
| Classification: 붓꽃(Iris) 데이터 분석하기 (1) | 2023.04.19 |
| Train data | Test data | Validation data 차이 (0) | 2023.04.19 |
| 과대적합(Overfitting)과 과소적합(Underfitting) (0) | 2023.04.18 |



