해당 글은 유튜브 채널(https://www.youtube.com/@Deeplearningai) 의 Machine Learning 강의를 정리한 글입니다.
일반적으로 모델의 복잡도를 키우고, 과적합을 막는 방법론을 사용한다고 했다. 과적합을 해결할 수 있는 3가지의 방법을 알아보자.
1. 더 많은 훈련 샘플 모으기
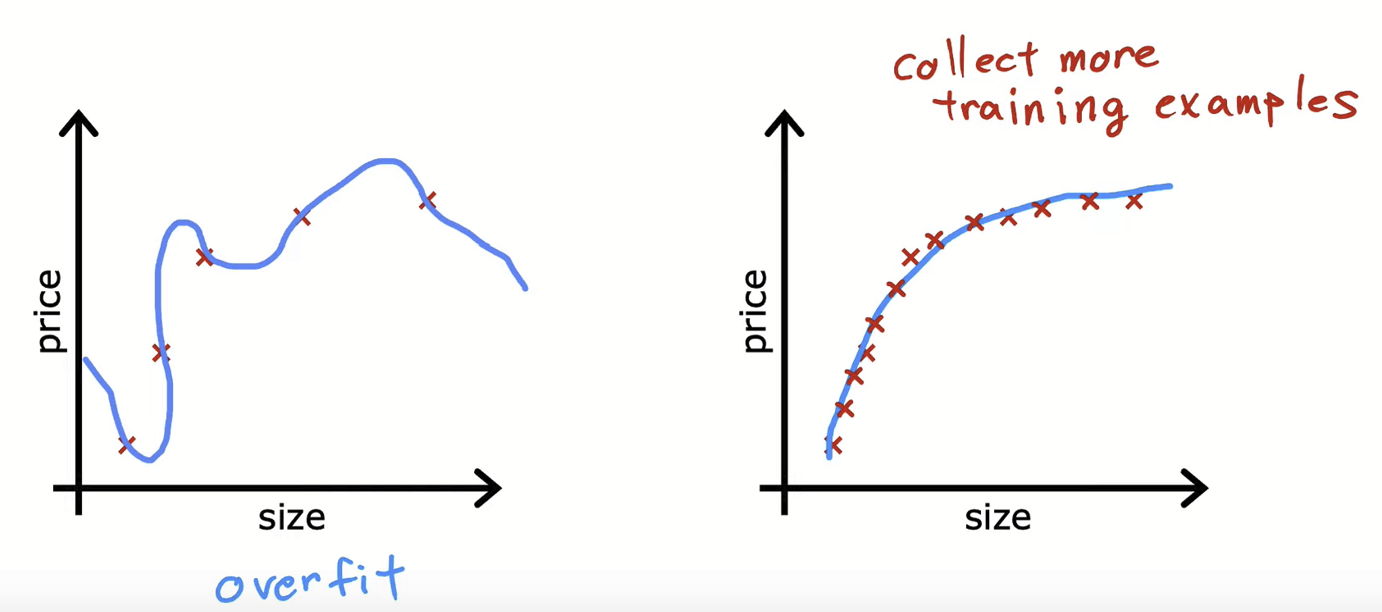
과적합의 경우 각 훈련 샘플에 너무 잘 맞다보니 곡선의 형태가 둘쑥날쑥하다. 더 많은 훈련 샘플을 모으면 그만큼 모델의 들쑥날쑥한 정도가 줄어들어 우측 그래프처럼 일정하게 완만히 올라가는 그래프의 형태를 얻을 수 있다.
2. 피쳐들 중에 몇 개만 선택하기
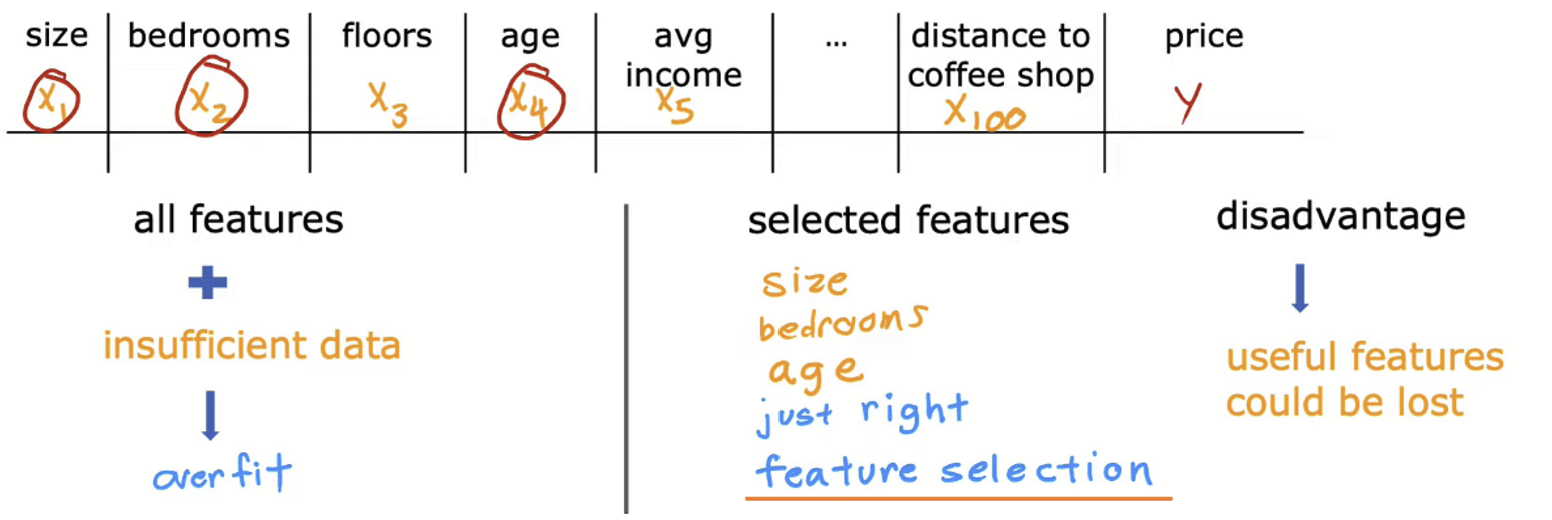
많은 피처에 비해 데이터셋이 충분치 않으면 과적합을 유발할 수 있으니 필요할 것만 같은 피쳐만 뽑자. 이렇게 예측값(y)에 가장 영향을 많이 끼칠 것 같은, 정말 필요할 것 같은 피쳐들만 뽑는 것을 Feature Selection 이라고 한다.
물론 몇 개의 피쳐들을 고른 만큼 제외되는 피쳐들이 있는데, 그 중에서 나름 중요했을 정보들도 포함되어 있는 피쳐를 잃을 수 있다는 단점이 있다. (예측을 위해, 정말 가장 중요한 피처들만 알아서 자동적으로 찾아주는 알고리즘도 존재한다고 한다.)
3. 가중치 규제(Weight Regularization)

과적합의 원인이 너무 큰 매개변수 w의 값이 될 수 있다. 왼쪽 처럼 큰 매개변수 값과 곱해지는 피쳐의 값을 0으로 만들게 매개변수 w = 0으로 만들어 주는 방법이 있는데, 이는 사실 하나의 피쳐를 없앤다는 뜻이니 두 번째 방법과 똑같아지는 것이다.
아예 매개변수의 값을 0으로 만드는게 아니라 Regularization은 해당 피처의 가중치의 영향을 줄이는 방식이다. 너무 큰 편향의 값도 줄여줄 수 있는데, 사실 편향은 줄이던 말던 큰 변화의 차이는 없으니 그대로 둬도 상관없다.
이제 가중치 규제가 어떻게 가중치의 영향을 줄이는지 보자.

비용함수에서 가중치가 컸던 $w_3$과 $w_4$에 큰 수를 곲한 값을 더해준다. 비용함수의 값을 최소화하는게 목적이니, 큰 값을 더해야 비용함수의 값을 최대한 작게 만들기 위해 $w_3$과 $w_4$의 값이 작아지기 때문이다.

비용함수를 파라미터의 임팩트를 고려하는 방향으로 바꿔주었다.위의 식은 1부터 n개까지의 피쳐, 즉 모든 피쳐의 가중치 값을 조정해주는 식이다. 이 때 람다는 우리가 직접 설정해주는 하이퍼파라미터다. (마지막에 추가하 편향 관련 규제는 넣어주지 않아도 된다.)
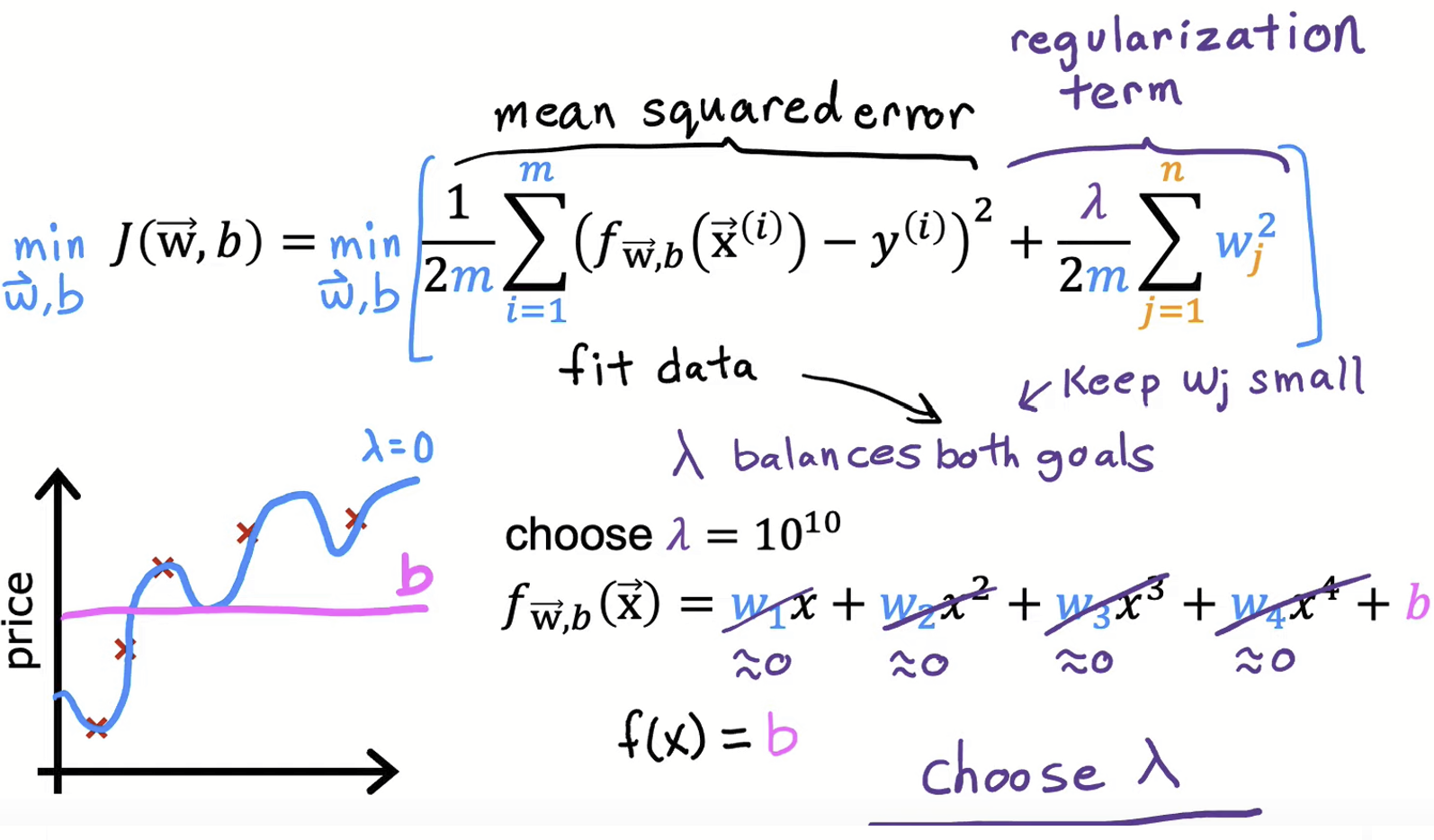
편향 부분을 빼고 새로 정리한 비용함수 식이다. Mean squared error를 통해 예측값과 실제값의 오차를 줄여나가며 데이터에 fit한 모델을 만들고, 과적합을 방지하기 위해 모든 가중치의 임팩트를 최소화시켜준다. 여기서 람다의 설정이 중요한데 람다를 $0$으로 두면정규화 과정이 사라지는 것이니, 모델의 형태는 바뀌지 않을 것이고, 그렇다고 $10^10$과 같이 굉장히 큰 수일 시에 그만큼 가중치 변수가 매우 작은, 거진 0에 가까운 값이 되어 피처가 없는 것과 마찬가지가 되어 f(x) = b와 같이 편향만 남게 된다. 이 경우엔 과소적합의 문제가 발생한다. 따라서 과적합도, 과소적합도 일으키지 않을 적당한 값으로 람다를 설정해 주는 것이 중요하다.

새로 정의한 비용함수를 경사 하강법에 적용한 것이다. 편향의 경우 가중치 규제를 적용하지 않았다.

복잡한 위의 식을 조금 더 간단하게 정리한 것이다. 정규화 과정에 대한 예시로 학습률= 0.01, 람다 =1, m =50(데이터 개수) 로 설정해 계산해보면 가중치 값에 0.9998이 곱해지게 된다. 즉 기존 가중치의 임팩트를 아주 조금 줄인 것이 된다.

Logistic Regression에서도 마찬가지다. Logistic Regression에서 사용되는 비용함수에 가중치 규제 식을 추가해주기만 하면 된다.
참고
https://www.youtube.com/@Deeplearningai
사진 출처
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| 지수 가중 평균(Exponentially weighted averages) (0) | 2023.05.17 |
|---|---|
| 경사하강법의 세 종류(BGD, SGD, MGD) (1) | 2023.05.17 |
| Linear Regression 과 Logistic Regression (0) | 2023.05.09 |
| Classification: 붓꽃(Iris) 데이터 분석하기 (1) | 2023.04.19 |
| Train data | Test data | Validation data 차이 (0) | 2023.04.19 |



