해당 글은 유튜브 채널(https://www.youtube.com/@Deeplearningai) 의 Improving Deep Neural Networks 강의를 정리한 글입니다.
Exponentially weighted averages(지수 가중 평균)
경사 하강법보다 빠른 몇 가지 최적화 알고리즘이 존재한다. 그 알고리즘들을 이해하기 위해서는 먼저 지수 가중 평균(Exponentially weighted averages)을 이해해야한다. (통계학에서는 지수 가중 이동 평균이라고도 부른다.)
지수 가중 평균(=지수 이동 평균)이란, 데이터의 이동 평균을 구할 때, 오래된 데이터가 미치는 영향을 지수적으로 감쇠(exponential decay) 하도록 만들어 주는 방법이다.
지수 가중 평균의 예

- 위의 그래프에는 런던 기온의 일별 기온 데이터가 파란 점으로 분포되어 있다.
- 이때 시간의 흐름에 따라 이 데이터가 어떻게 움직이는가에 대한 경향선을 보고싶다고 가정해보자.
- 단순하게 전후 며칠간의 평균으로만 계산한다면, 오래된 데이터의 영향과 최신 데이터의 영향이 비슷해져서 우리가 원하는 추세를 나타낼 수 없을 것이다.
- 이를 보완하기 위해 오래된 데이터와 최신 데이터에 Weight을 부여하는 방식이 도입되었는데,
- 시간의 흐름에 따라 오래된 데이터의 영향이 지수적으로 감쇠하도록 설계한 방식으로 지수 가중 평균 방식이라 한다.
데이터의 지역 평균이나 이동 평균의 흐름을 계산하고 싶다면 다음과 같은 방법이 있다.
1) $v_0 = 0 $ | $v_0$을 0으로 초기화한다.
2) v라는 날에 대한 공식의 일반화는 전날의 온도 * 0.9 + 그 날의 온도 * 0.1 이다.
$v_0 = 0$
$v_1 = 0.9*v_0+0.1*θ_1$
$v_2 = 0.9*v_1+0.1*θ_2$
$\cdots$
$v_n = 0.9*v_{n-1} +0.1*θ_n$
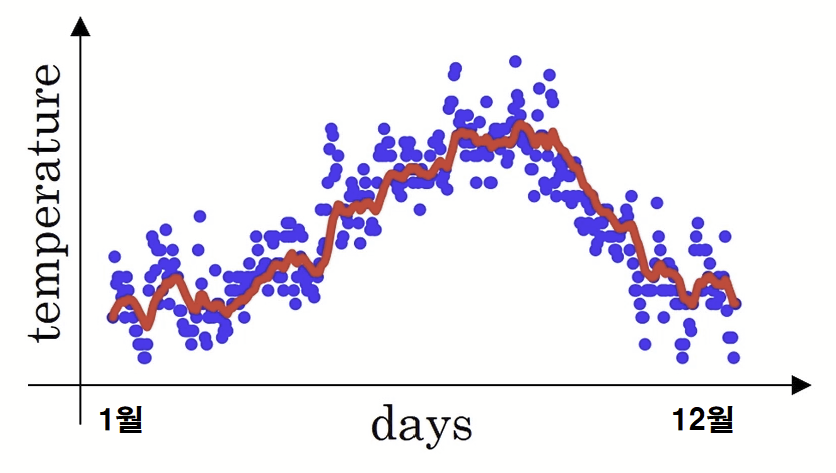
그래프의 빨간색 선이 지수 가중 평균 방식으로 구한 일별 기온의 이동평균을 나타낸다.
Understanding Exponentially weighted averages
지수 가중 평균 식
$v_t = \beta *v_{t-1} + (1- \beta)*θ_t$
( $0 \leq \beta \leq 1$, $θ_t$: 새로 들어온 데이터, $v_t$: 현재의 경향)
➱ $\beta$ 는 하이퍼파라미터로 0~1사이의 값을 갖는다.
➱ $\beta *v_{t-1}$은 과거의 경향성이고, $(1- \beta)*θ_t$ 는 새로운 경향성이라고 이해할 수 있다.
왜 '지수적' 감쇠라고 부르는지, 이해를 위한 예시를 가져왔다.(예시 속 $\beta = 0.9$)

이해를 돕기위해 세타 관련식과 베타 관련식의 위치를 바꾼 것이다. 맨 아래 식을 보면 0.9인 $\beta$가 더 오래된 데이터일수록 더 많은 제곱이 붙어 더 작아지고 있음을 알 수 있다.
- $\beta$값이 0과 1사이니 제곱이 되었을 때 더 작아진다는 것.
- 따라서 오래된 데이터일수록 현재의 경향을 표현하는 데 더 적은 영향을 미치게 됨을 의미한다.
- 이렇듯, 오래된 데이터는 $\beta$의 n제곱만큼 지수적으로 값이 빠르게 감소하기 때문에 이를 "지수적(Exponentially) 감쇠"라고 부른다.
지수 가중 평균의 근사
지수 가중 평균의 근사 식
$v_t \approx \frac{1}{(1-\beta)} $
- $v_t$값은 근사적으로 1/(1 - β) 일 간의 데이터만을 사용해 평균을 취하는 것과 같다고 한다.
- 예를 들어,
- β = 0.9 → 1 / (1 - 0.9) = 10이니 10일간의 데이터를 가지고 가중평균을 구한 것.
- (즉 10일간의 온도의 평균이 해당 날짜의 $v_t$값인 것이다.)
- β의 값이 1에 근사할수록 사용한 데이터의 기간이 길다는 것인데, 그만큼 오래된 날의 β값은 굉장히 많은 제곱된 상태니 거진 0에 근사하게 되어 현재의 경향성을 표현하는 것에 영향을 미치지 못한다.

▹ 빨간색 그래프: β = 0.9 → 10일간의 가중평균
▹ 초록색 그래프: β = 0.98 → 50일간의 가중평균
▹ 노란색 그래프: β = 0.5 → 2일간의 가중평균
- 값이 1에 가까워, 더 많은 날들을 고려하기 때문에 더 부드러운 곡선 모양의 그래프가 나온다.
- 더 큰 범위(50일)에서의 기온을 평균하기 때문에 원래 데이터 샘플 값에서 더 멀어지게 되었다.
- = 0.98이니 이전 데이터(과거)의 경향인 $v_{t-1}$에 큰 가중치를 주고 현재의 데이터 $θ_t$에는 0.02 만큼의 가중치만 주게 되니 최신 데이터보다는 과거의 데이터에 대한 비중이 크다.
이 매개변수 "β" 혹은 학습 알고리즘의 하이퍼파라미터의 값을 바꿈으로써 위처럼 약간씩 다른 효과를 얻게 되는데 그 중에서 가장 만족스러운 효과가 좋았단 값으로 β를 설정해주면 된다.
Bias Correction (편향 보정)
지수 가중 평균을 어떻게 구현하는지 배워봤는데, 편향 보정이라고 불리는 기술적인 세부 사항으로 평균을 더 정확하게 계산할 수 있어진다. 어떻게 작동되는지 살펴보자.
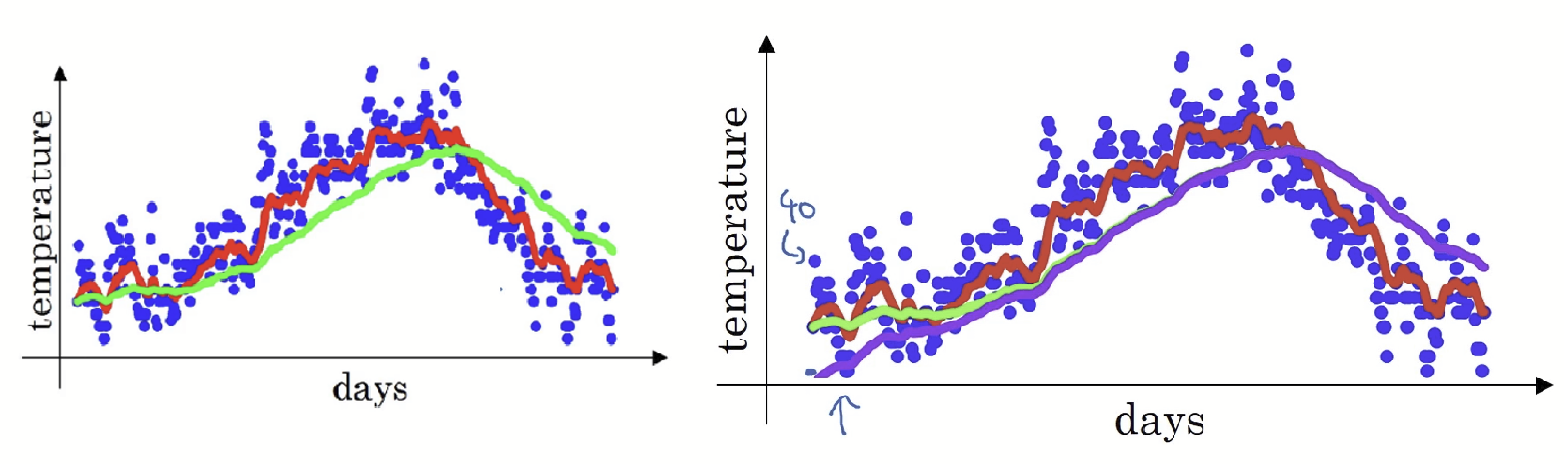
= 0.98 일때의 그래프가 왼쪽 그래프의 초록색 그래프라고 했었는데, 사실 $v_t = \beta *v_{t-1} + (1- \beta)*θ_t$ 대로 구하면 해당 그래프의 모습을 얻을 수 없다. 그 대신 오른쪽 그래프에서 보이는 저 보라색 곡선을 얻게 된다.
첫 번째 날의 온도를 화씨 40도라 했을 때($v_1 = 40$), 공식대로 계산하면
$v_0 = 0$
$v_1 = 0.98*v_0(= 0) + (1 - 0.98)*θ_1(= 40) ➱ v_1 = 0 + 0.02 * 40 = 0.8$
온도가 40도와는 너무 거리가 먼 0.8도가 나오게 된다. 즉 제대로 추정이 불가능한 상태인 것이다. 이렇듯, 보라색 곡선의 그래프를 보면 초기 구간이 원래 데이터 샘플값과 거리가 유독 먼데 그래서 보통 머신러닝에서는 지수 가중 평균을 구현할 떄, 그냥 이렇게 차이가 많이 나오는 초기 구간을 기다린 다음에 지수 가중 평균을 사용한다고 한다. 따라서 편향 보정을 신경쓰지 않는다고 한다.
하지만 초기 구간의 편향이 신경 쓰인다면 다음과 같이 편향 보정을 사용해주면 된다.
$v_t(biascorrection)$
$= v_t / (1 − β_t)$
$= \frac{β*v_t−1 + (1 − β)*θ_t}{(1 − β_t) } $
위의 식을 사용해 v_t 의 편향이 보정된 값으로 다시 구해보면
$v_1 = 0 + 0.02 * 40 = 0.8$
$v_1(biascorrection) = 0.8 / (1 - 0.98) = 40$
원래 데이터 샘플 값인 40이 그대로 나오는 것을 볼 수 있다.
이처럼 편향 보정은 초기 단계의 학습에서 더 나은 온도의 추정값을 얻을 수 있도록 도와준다.
(즉, 보라색 그래프에서 초록색 그래프로 갈 수 있게 해주는 것.)
참고
https://wooono.tistory.com/225
https://velog.io/@minjung-s/Optimization-Algorithm
https://www.youtube.com/@Deeplearningai
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| Feature Scaling (ft. 입력 특성 정규화하기) (0) | 2023.05.19 |
|---|---|
| 최적화 알고리즘 (ft. Momentum, RMSprop, Adam) (1) | 2023.05.18 |
| 경사하강법의 세 종류(BGD, SGD, MGD) (1) | 2023.05.17 |
| 가중치 규제 (Weight Regularization) ft. 과적합 해결하기 (0) | 2023.05.09 |
| Linear Regression 과 Logistic Regression (0) | 2023.05.09 |



