최적화 알고리즘 (ft. Momentum, RMSprop, Adam)

경사 하강법보다 빠른 몇 가지 최적화 알고리즘이 존재한다. 그 알고리즘들을 이해하기 위해서는 먼저 지수 가중 평균(Exponentially weighted averages)을 이해해야한다

지수 가중 평균에 대한 글은 아래 글을 참조해주세요.

지수 가중 평균(Exponentially weighted averages)

 

Gradient descent with momentum

모멘텀 알고리즘이란, 경사 하강법에서 기울기(gradient)의 가중 평균치를 산출하여 가중치(Weight)를 업데이트하는 것이다. 다르게 표현하자면, 원래 현재 시간의 gradient를 이용해서만 weight를 업데이트한 것과 다르게 Momentum 기반의 SGD는 이전 시간의 gradient 들까지도 고려하여 가중치를 업데이트 한다는 것이다.

 

위는 확률적 경사 하강법에서 최적의 해(빨간 점)를 찾는 과정을 나타낸 그림이다. 지그재그로 그려진 저 변동폭은 학습률(Learning rate)을 나타내며, 학습률이 작다면 학습속도가 너무 느릴 것이고, 그렇다고 학습률을 크게 설정한다면, over shooting이나 diverging 이 될 가능성이 있다. 따라서 최적화 과정에서 저 그래프의 가로축은 빨리 최적해에 도달하고 싶으니 빠른 학습을 원하는 반면, 세로축은 학습률이 크면 over shooting되거나 발산될 확률이 커지니 학습이 더 느리게 진행되길 바란다. 

 

위처럼 크게 삐쭉빼쭉한 지그재그의 길을 도함수에 대한 지수 가중 평균치를 구해서 부드럽게? 해 줄 수 있다.

 

Gradient Descent Algorithm (기존의 경사 하강법)
$w=w−α∗\frac{d}{dw}∗ J(w,b)  $
$b=b−α∗\frac{d}{db}∗ J(w,b)$       α : learning rate

 

Gradient Descent with Momentum
$v_{dw}  =  \beta *  v_{dw} + (1-\beta) *dw$     | 이때,   $dw =  \frac{d}{dw}∗ J(w,b)$
$v_{db}   =  \beta *  v_{db} + (1-\beta) *db$      | 이때,   $db =  \frac{d}{db}∗ J(w,b)$

$w = w − \alpha ∗ v_{dw}$
$b = b − \alpha ∗ v_{db}$

 

Momentum이 추가된 경사하강법에선 학습률을 가리키는 α 뿐만이 아니라 momentum의 β 하이퍼파라미터가 추가된다. 이때 β는 지난 몇개의 기울기 강하의 평균치를 사용할 것인가에 대한 파라미터로 보통 값으로 0.9를 많이 사용한다. (즉 10개의 기울기 강하의 평균치를 사용하겠다는 것)

 

출처: https://medium.com/analytics-vidhya/momentum-rmsprop-and-adam-optimizer-5769721b4b19

 

직관적으로 말하면, 이 Momentum 항을 추가함으로써 기울기가 훈련 중에 일종의 속도 v(Velocity)를 구축하도록 하게 하는 것이다. v는 가중 기울기의 누적 합계며  β는 속도를 약간 느리게 해주는 마찰로 생각할 수 있다. 

모멘텀 항을 사용하면 안장점과 local Minimum에 빠질 위험이 덜해지게 된다. 이는 Global optimal 로 가는 방향에 더 집중하게 되었다는 소리로, 더 이상 현재 지점에서의 손실 함수에 대한 기울기에만 의존하지 않고, 시간이 지남에 따라 축적된 속도에도 의존하게 되었기 때문에 가능하게 된 것이다. 다시 말해, 주어진 지점에서의 기울기 방향보다 축적된 속도가 나타내는 방향으로 더 많이 움직인다는 것이다.

 

언덕을 내려가는 공을 생각해보자. 시간이 지남에 따라 속도를 얻을 것이고 이때 이 속도는 모멘텀 항(v)를 나타내고 내려감에 따라 얻게 되는 가속은 dw가 제공한다고 볼 수 있다. 아무튼 최적해를 항해 공이 굴러가다보면 경사가 없는 구멍(Local minimum)이나 때로는 평평한 지면(Plateau)을 마주하게 될 텐데 이때까지 축적된 속도 v를 통해 공이 그 장애물을 넘어갈 수 있게 만들어 주는 것이다.

 

검정 선: SGD, 파랑 선: SGD with Gradient    /    출처: https://artemoppermann.com/de/optimierung-in-deep-learning-adagrad-rmsprop-adam/

 

확률적 경사하강법과 모멘텀이 추가된 확률적 경사 하강법을 직접 비교해본 영상이다. 파란색 부분이 손실함수의 값이 높은 부분이고 더 진한 빨간색일 수록 손실함수의 값이 낮은, 최적의 해와 가까운 곳을 의미한다.

모멘텀이 추가된 경우 지그재그 왓다갓다 거리는 움직임도 적어지고 훨씬 학습 속도가 빠르다는 것을 볼 수 있다.

 

 

RMSprop Algorithm (Root Mean Square Propatation)

SGD는 파란 그래프처럼 동작한다. 앞에서 말했듯, 안정적으로 global optimal로 향하기 위해서는 가로축으로는 빠르게 전진해야하고, overshooting 과 diverging 문제를 피하고 싶으니 세로축으로는 학습이 천천히 진행되길 바란다고 했었다.

 

이때 위 그림에서의 명료성을 위해 가로축을 dw, 세로축을 db라 칭하고 설명하겠다.

 

일단, RMSprop 알고리즘은 다음과 같다.

RMSprop Algorithm
$s_{dw}  = β_2*s_{dw}  + (1-β_2)*dw^2$ 
$s_{db}  = β_2*s_{db}  + (1-β_2)*db^2$

$w ≔ w - α* \frac{dw}{( \sqrt{s_{dw}} + ε)}$
$b ≔ b - α* \frac{dw}{( \sqrt{s_{db}} + ε)} $

s는 지수가 평균을 나타내며 $β_2$는 모멘텀의 하이퍼파라미터인 β 와 구별하기 위해 2를 추가로 표기한 것이다.

ε 은 0으로 나눠지지않도록 하기 위한 수학적 안전성을 위해 추가한 값이다.(ε = 10^(-8)이  합리적인 기본값이라 한다.)

 

RMSprop 최적화 기법에서 우리는 가중치 w 방향으로의 이동이 'b' 방향으로의 이동보다 크도록 매개변수를 업데이트하고 싶은 것이다. 세로축인 수직에서의 경사가 크니 db가 dw다 큰 값을 가지는데, 따라서 dw²도  db²보다 작으므로 dw의 지수 평균이 db보다 작다. ($s_{dw} < s_{db}$)

따라서 그래디언트를 각각의 지수 평균의 근으로 나누면 'w'의 업데이트가 'b'의 업데이트보다 크다. 이렇게되면 수평 방향으로 더 큰 스텝을 가서 더 빠르게 수렴할 수 있다. 또한 db를 더 큰 숫자로 나눠서 업데이트하기 때문에 진동을 줄이는데에도 도움을 준다. 도함수를 제곱해서 제곱근을 얻기 때문에 Root Mean Squared Propagation이라는 이름을 가진다.

 

 

Adam Optimization Algorithm (Adaptive Moment Estimation)

아담(Adam)은 모멘텀과 RMSprop을 섞어 놓은 최적화 알고리즘으로, 딥러닝에서 가장 흔히 사용되는 최적화 알고리즘 이다.

 

Adam Optimization Algorithm

1). 먼저 초기화를 진행하고, Momentum과 RMSprop에서 사용한 v와 S를 지정해준다.

$v_{dw​} ​= 0, s_{dw}​​ = 0, v_{db} ​​= 0, s_{db} ​​= 0$

$v_{dw}  =  \beta *  v_{dw} + (1-\beta) *dw$  
$v_{db}   =  \beta *  v_{db} + (1-\beta) *db$  
$s_{dw}  = β_2*s_{dw}  + (1-β_2)*dw^2$ 
$s_{db}  = β_2*s_{db}  + (1-β_2)*db^2$

 

2). 편향 보정(Bias Correction)도 추가해준다.

$v^{biascorr}_{dw}= \frac{v_{dw}}{(1 − β^t)}$
$v^{biascorr}_{db}= \frac{v_{db}}{(1 − β^t)}$
$s^{biascorr}_{dw}= \frac{v_{dw}}{(1 − β^t)}$
$s^{biascorr}_{db}= \frac{v_{db}}{(1 − β^t)}$

 

3) Momentum과 RMSprop을 모두 사용하여 가중치 업데이트를 진행한다.

$w := w - \alpha * \frac{v^{biascorr}_{dw} }{ \sqrt{s^{biascorr}_{dw}} + \varepsilon }$
$b := b - \alpha * \frac{v^{biascorr}_{db} }{ \sqrt{s^{biascorr}_{db}} + \varepsilon }$

 

 

여러 최적화 알고리즘의 성능 비교 / 출처: https://www.i2tutorials.com/explain-about-adam-optimization-function/

 

 

 

The Problem of Local Optima

딥러닝 학문의 초기에는 최적화 알고리즘이 많이 발달하지 않아 지역 최적값(Local minimum)에 빠질 위험성이 있었다. 지금까지 딥러닝 이론이 발전하면서 최적화 알고리즘은 많이 발달하게 되었고 사실 고차원 공간에서 정의되는 Loss function에 대하여 Local minimum에 빠질 확률은 매우 낮다. 예로 20,000차원의 공간에서 지역 최적값이 되기 위해서는 20,000개의 방향에서 그래프가 위로 볼록하던지, 아래로 오목하던지 하나의 방향으로 확실해야 하기 때문이다. 이는 네트워크를 구성하는 모든 매개변수가 Local minimum 을 가져야 지역 최적값 문제에 빠진다는 뜻으로, 그럴 확률은 당연히 희박하다. 따라서 Local minimum은 그다지 고려하지 않는다.

 

실제로 고차원에서 경사가 0인 지점은 대부분은 Local minimum이 아니라 안장점(Saddle point)이다. (말 그대로 그래프가 말의 안장처럼 생겨서 붙여진 이름이다.) 오른쪽 그래프를 보면 알 수 있듯, 말 안장점은 보는 지점에 따라 최소값이 될 수도, 최대값이 될 수도 있으니 최적점이라 할 수 없다.

 

 

 

The Problem of Plateaus

 

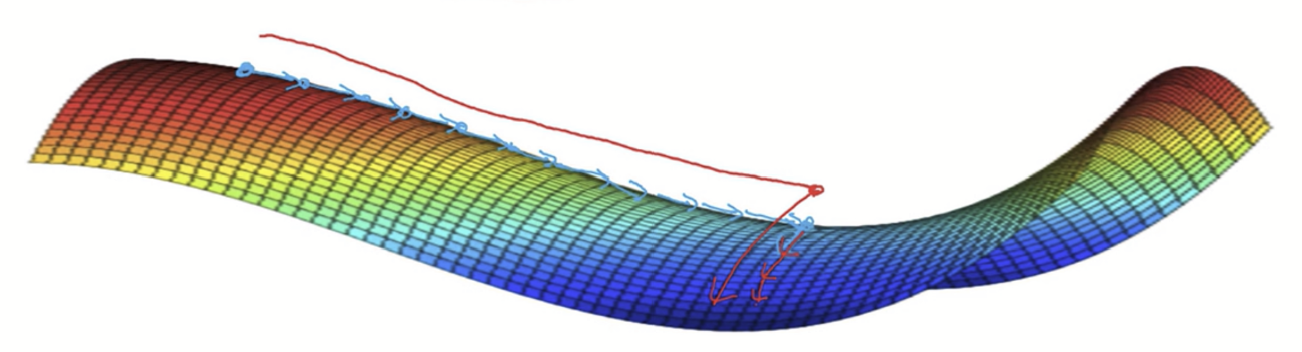
즉 진짜 문제는 Local minimum이 아니라 위와 같은 모습의 Plateaus 다. Plateaus는 미분값이 아주 오랫동안 0에 가깝게 유지되는 지역을 말한다. 위처럼 경사가 거진 없는, 0에 가까울 경우 면이 거의 평평해서 학습하기까지 아주 오랜 시간이 걸리게 된다.

이때 앞서 설명한 Momentum, RMSprop, Adam 등과 같은 알고리즘을 통해 Plateaus 에서 벗어나게 할 수 있다.

 

 

plateaus에 취약한 SGD, 그에 반해 다른 최적화 알고리즘은 plateaus에서 벗어나고 있다.

 

 

 

 

 

 

참고

https://untitledtblog.tistory.com/149

https://velog.io/@minjung-s/Optimization-Algorithm

https://medium.com/analytics-vidhya/momentum-rmsprop-and-adam-optimizer-5769721b4b19

https://artemoppermann.com/de/optimierung-in-deep-learning-adagrad-rmsprop-adam/

https://www.youtube.com/watch?v=lWzo8CajF5s&list=PLkDaE6sCZn6Hn0vK8co82zjQtt3T2Nkqc&index=19