반응형
Normalizing training sets

신경망의 훈련을 빠르게 할 수 있는 하나의 방법중에 입력으로 들어오는 Feature들을 정규화(Normalizing)이 있다.
위의 표는 두 개의 입력 특성을 가진 훈련 데이터 세트의 분포(산포도)를 나타낸 표다. 두 단계에 따라서 입력을 정규화한다.
1). 데이터 세트의 평균을 0으로 만든다.
- μ = 1/m 곱하기 1부터 m까지 $x^{(i)}$의 합으로 평균값을 나타내는 벡터다.
- x는 그럼 모든 훈련 데이터에 대해서 x-μ로 설정된다. (원래 값에서 평균값을 빼주는 것)
- 0의 평균을 갖게 될 때까지 훈련 세트를 이동한다.
2). 분산을 정규화한다.
- 아직 특성 x1이 x2보다 더 큰 분포도를 가지니, 이 둘을 맞춰주기 위해 분산을 정규화한다.
- $σ^2$ = 1/m 곱하기 1부터 m까지 $x^(i)**2$의 합으로 설정한다. (**은 요소별 제곱을 나타냄)
- $σ^2$는 각 특성의 분산에 대한 벡터다
- 이 값을 아까 x-μ 에서 얻은 새 x 값에서 나눈다.
- 이렇게 x1과 x2의 분산은 같아진다.
Feature 정규화에 대한 추가적인 설명은 아래 글을 참고해주세요.
Feature Scaling (ft. 입력 특성 정규화하기)
해당 글은 유튜브 채널(https://www.youtube.com/@Deeplearningai) 의 Machine Learning강의를 정리한 글입니다. 집의 크기와, 방의 개수에 따라 집의 가격을 예측하는 다중 선형 회귀 모델이다. 집의 사이즈의 범
bruders.tistory.com
그렇다면 입력 특성뿐만이 아니라 신경망의 은닉충에서 계산되는 값들도 정규화를 해주면 어떨까?
배치 단위 학습의 문제점
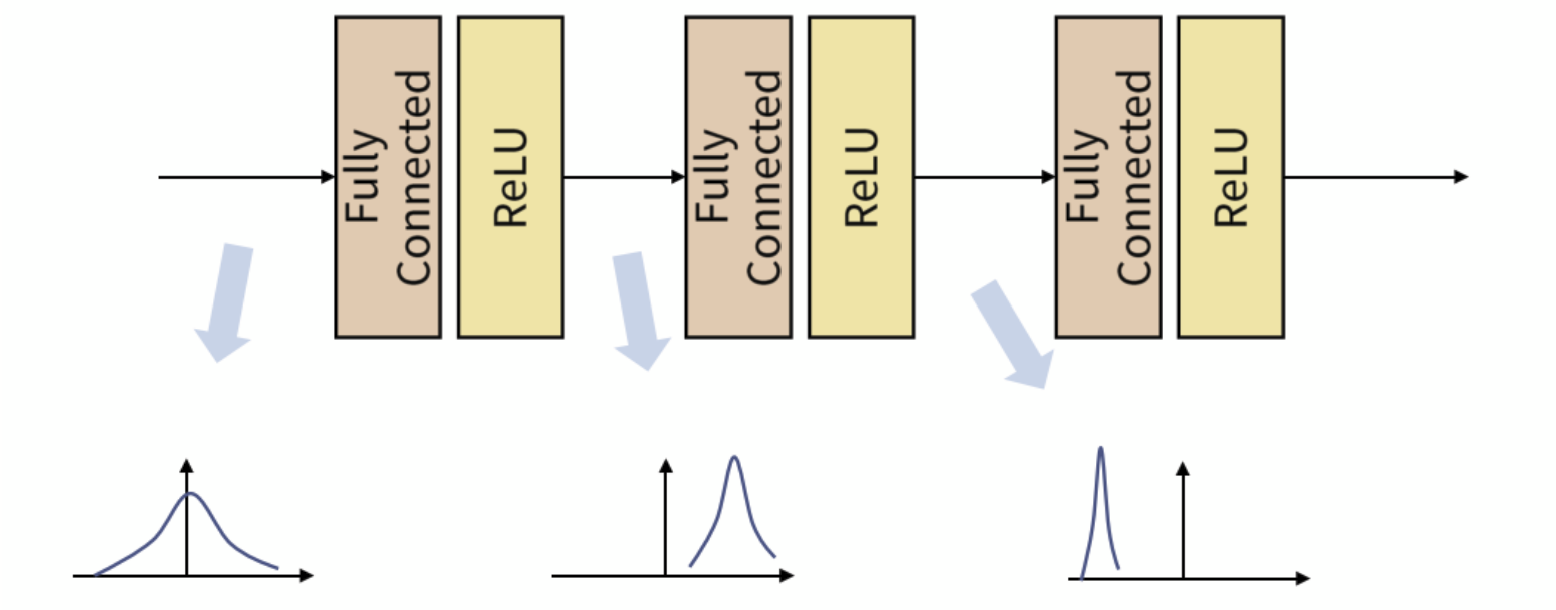
- Batch 단위로 학습을 하게 되면 Internal Covariant Shift 란 문제점이 생긴다.
- Internal Covariant Shift 는 위와 같이 학습 과정에서 계층 별로 입력의 데이터 분포가 달라지는 현상을 말한다.
- 각 계층에서는 입력을 받고 convolution이나 위와 같이 fully connected 연산을 거친 뒤 활성화 함수(Activation function)을 적용하게 되는데 이때 연산 전/후에 데이터 간 분포가 달라질 수가 있다.
- 이와 유사하게 Batch 단위로 학습을 하게 되면 Batch 단위간에 데이터 분포의 차이가 발생할 수 있다. ( 즉 Batch 간의 데이터가 상이한 것.)
- 이 문제를 개선하기 위해 Batch Normalization 개념이 적용된다.
Batch Normalization (BN) | 배치 정규화

- Sergey Ioffe와 Christian Szegedy가 만든 알고리즘이다.
- 신경망을 학습시킬 때, 보통 전체 데이터를 한 번에 학습시키는 것은 오래걸리니, 여러 집단으로 분할해서 학습을 시키는데, 이 때 하나의 집단이 배치(Batch)다.
- 따라서, 배치 단위로 정규화하는 것을 배치 정규화라고 부른다.
- 배치들은 학습을 진행하며, 각 Hidden layer의 활성화 함수 입력값 또는 출력값에서 정규화된다.
- (실제로는 활성화 함수의 입력값을 정규화하는 것이 흔하다고 한다.)
- 배치 정규화를 통해서도 근본적으로 학습과정을 안정화할 수 있고 빠르게 할 수 있다.

- 배치 정규화를 통해 입력 값의 다른 분포를 일정하게 만들어줄 수 있다.
- 위는 정규화를 통해 분포를 Zero mearn gaussian 형태로 만든 것으로, 데이터의 분포를 평균을 0, 표준 편차는 1로 조정한 것.
이론

- 깊은 신경망일수록 같은 Input 값을 갖더라도, 가중치가 조금만 달라지면 완전히 다른 값을 얻을 수 있다.
- Training 셋의 분포와 Test 셋의 분포가 다르면 학습이 안되는 것처럼 같은 학습 과정 속에서도 각 layer에 전달되는 feature의 분포가 다르게 되면 학습하는 데 어려움이 생긴다.
- 이러한 문제는 training 할 때 마다 달라지게 되고 Hidden Layer의 깊이가 깊어질수록 변화가 누적되어버려 feature의 분포 변화가 더 심해지게 된다.
- 이를 해결하기 위해, 각 layer에 배치 정규화 과정을 추가해준다면, 가중치의 차이를 완화하여 보다 안정적인 학습이 이루어질 수 있다.
알고리즘

- Hidden Layer의 활성화 함수의 입력값으로 들어오는 배치의 평균과 분산을 계산한다.
- 해당 배치가 평균값으로 0, 분산으론 1을 갖도록 정규화한다. (ε는 분모가 0이 되는 것을 막기 위한 아주 작은 숫자($1e^{-5}$))
- 정규화 이후, 배치 데이터들을 Scale(감마(γ)), Shift(베타(β)) 를 통해 새로운 값으로 바꾼다.
감마와 베타를 통해 Scaling과 Shifting을 하는 이유
- 정규화를 통해 평균이 0 분산을 1로 고정이 된다고 생각해보자.
- 이때 활성화 함수의 비선형 성질을 잃게 되는 문제가 발생한다.

- 입력 값이 N(0, 1) 이라면, 대부분의 입력값은 Sigmoid 함수 그래프의 중간 (x = (-1.96, 1.96) 구간)에 속하게 된다.
- 저 초록 사각형에 해당하는 부분으로, 선형을 띄기 때문에 비선형 성질을 잃게 되는 것이다.
- 하지만, 감마(γ), 베타(β)를 통해 활성함수로 들어가는 값의 범위를 바꿔줌으로써, 비선형 성질을 보존하게 된다.
- 감마(γ), 베타(β) 값은 학습 가능한 변수이며, Backpropagation을 통해서 학습이 된다.
테스트 단계
- 배치 정규화는 한 번에 하나의 미니배치에 속한 데이터를 처리한다.
- 하지만 테스트 단계에서는 미니배치가 존재하지 않으니 한 번에 샘플 하나씩 처리해야 한다. 하지만 하나의 샘플로 평균과분산을 구하는 것은 당연히 의미없다.
- 따라서 테스트 단계에서는 전체 Training Set의 평균과 분산을 사용한다.
- 하지만 엄청나게 많은 전체 Training set에 대한 평균과 분산을 계산하는 것은 무리니,
- 아래의 식처럼 모델의 학습 단계에서 사용한, 각 n개의 미니배치에 대한 평균과 분산을 이용해, 전체 Training Set의 평균과 분산을 대신할 수 있다.

- 위와 같은 방법 대신, 미리 저장해둔 n개의 미니 배치의 이동 평균을 사용하여 해결할 수 있다.

- 따라서 모델 학습 단계에서 매 미니배치마다 이동 평균과 분산을 저장해 두어야 한다.
- 그래야 테스트 때, 모델 학습 단계에서 저장한 이동 평균과 분산을 사용할 수 있다.
- 식에서 α값은 일반적으로 1에 가까운 0.9, 0.99, 0.999로 설정한다.
참고
https://wooono.tistory.com/227
https://gaussian37.github.io/dl-concept-batchnorm/
https://www.youtube.com/@Deeplearningai
728x90
반응형
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| [논문리뷰] Transformer (Attention Is All You Need) (0) | 2023.05.29 |
|---|---|
| Feature Scaling (ft. 입력 특성 정규화하기) (0) | 2023.05.19 |
| 최적화 알고리즘 (ft. Momentum, RMSprop, Adam) (0) | 2023.05.18 |
| 지수 가중 평균(Exponentially weighted averages) (0) | 2023.05.17 |
| 경사하강법의 세 종류(BGD, SGD, MGD) (1) | 2023.05.17 |