해당 글은 wikidocs의 16 - 01 트랜스포머(Transformer)에 대한 글을 정리한 글입니다.
기존 Seq2Seq 모델의 한계
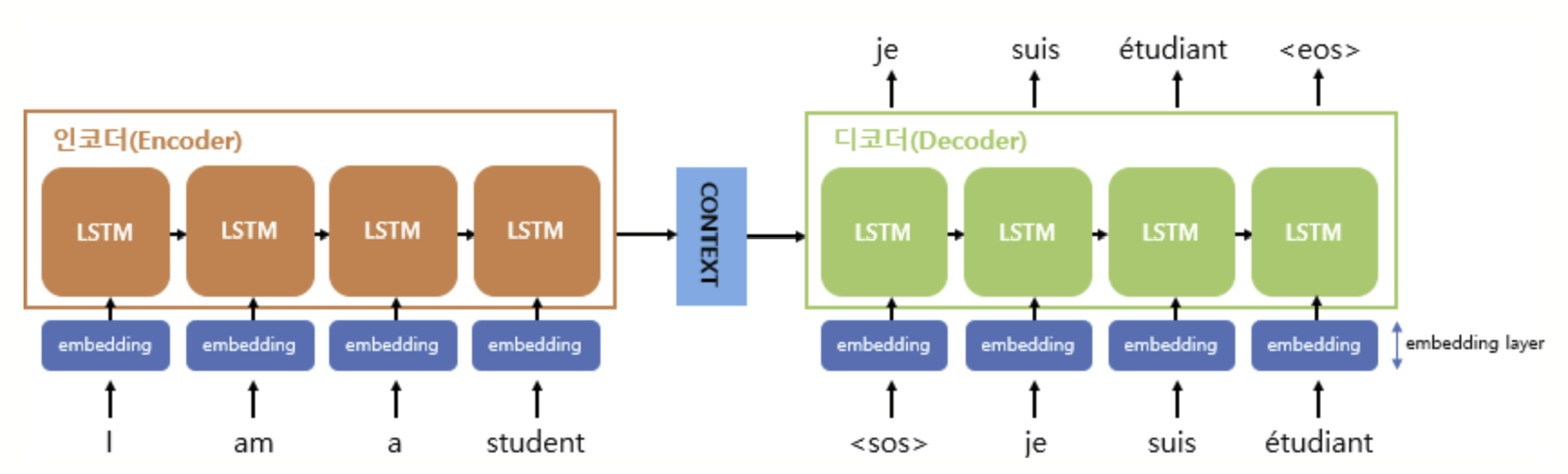
Seq2Seq2 모델은 위와 같은 모습을 가진다. 인코더 파트에서는 입력 문장의 모든 단어들을 순차적으로 입력받고, 마지막에 단어들로부터 얻은 모든 정보들을 압축해서 하나의 벡터로 만든다. 이 벡터를 컨텍스트 벡터(Context Vector)라 부른다. 이 Context Vector는 입력 문장에 대한 문맥적인 정보를 담게 되는데 디코더는 해당 벡터를 받아 번역된 단어를 한 개씩 순차적으로 출력한다.
한 단어에 대한 계산은 앞에 단어에 대한 계산이 끝나야 가능하니 정보의 흐름에 병목 현상(Bottleneck)이 일어날 수 있다는 문제점이 있다. 입력 문장의 길이가 짧던, 길던 고정된 크기를 가진 Context Vector에 정보를 압축하려다 보니 이 또한 전체 성능에서 병목 현상의 원인이 될 수 있다.
➱ Transformer Architecture 를 통해 전체 시퀀스에 대해 더 많은 계산을 병렬로 처리할 수 있게 되었다.
Word Embedding 이란?

워드 임베딩(Word Embedding)이란 위와 같이 사람이 쓰는 자연어를 기계가 이해할 수 있게 숫자의 나열인 벡터로 바꾸는 것을 말한다. 예시에서는 작은 4차원으로 표현했지만 실제 임베딩 벡터는 수백개의 차원을 가질 수 있다.
기계 번역 발전 과정
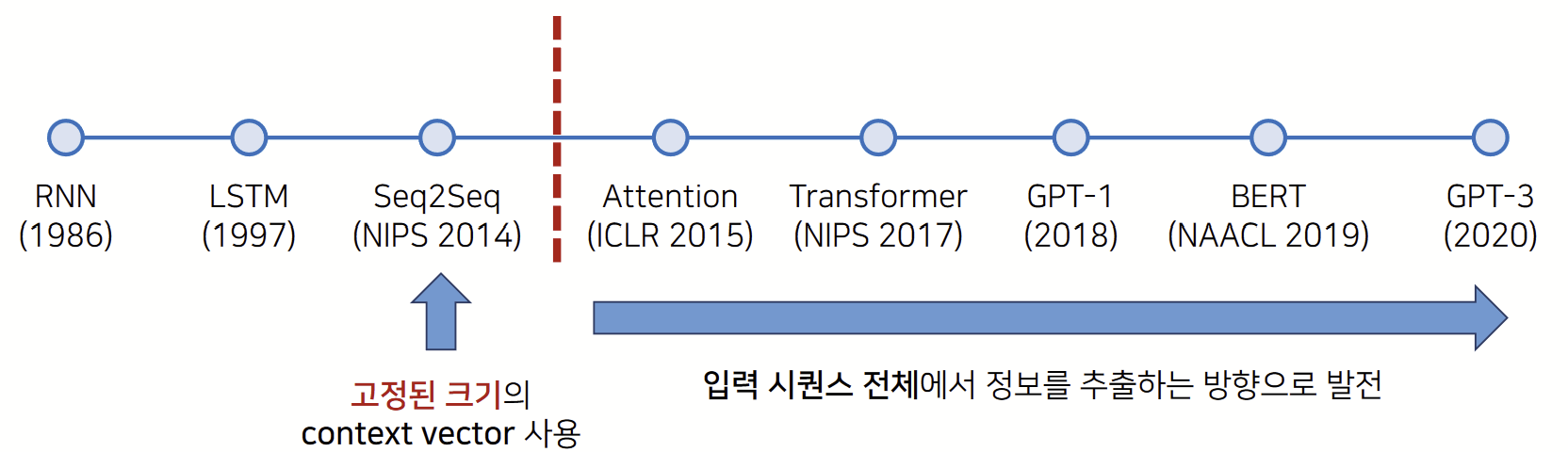
2021년 기준으로 최신 고성능 모델들은 Transformer 아키텍처를 기반으로 하고 있다.
• GPT: Transformer의 디코더(Decoder) 아키텍처를 활용
• BERT: Transformer의 인코더(Encoder) 아키텍처를 활용
Attention 메커니즘이 나온 이후 더 이상 RNN 기반의 아키텍처를 사용할 필요가 없어졌다.
트랜스포머 (Transformer)

트랜스포머는 왼쪽의 그림과 같은 구조를 가진다.
특징
- RNN을 전혀 사용하지 않는다.
- 대신 추가로 Positional Encoding을 해준다.
- 기존의 seq2seq처럼 인코더-디코더 구조를 가진다.
- 인코더와 디코더가 여러번 중첩된 구조다.
- (논문에서는 각각 6개의 인코더와 디코더를 사용함. 보통 인코더와 디코더의 개수를 같게 설정하지만, 무조건 같을 필요는 없다.)
이제 트랜스포머의 동작 원리를 차근차근 알아보자.
포지셔널 인코딩(Positional Encoding)

RNN는 단어의 위치에 따라 단어를 순차적으로 입력을 받아 처리해 각 단어의 위치 정보(Position Information)를 가질 수 있는데, 트랜스포머는 RNN을 가지지 않으니 인코더의 Attention 과정을 진행하기 전에 입력으로 들어갈 단어의 임베딩 벡터에 위치 정보를 더해줘야 한다. 이를 포지셔널 인코딩(positional encoding)이라고 한다.

하나의 문장에 포함된 각각의 단어들의 상대적인 위치 정보를 모델에게 알려주기 위해 transformer 에서는 사인, 코사인 같은 주기함수를 사용한다. (꼭 사인이나 코사인 함수일 필요는 없으며 주기성을 학습할 수 있도록 한다면 어떠한 함수의 사용도 가능하다고 한다.)

- $pos$ : 입력 문장에서의 임베딩 벡터의 위치
- $i$: 임베딩 벡터 내의 차원의 인덱스
- 인덱스가 짝수인 경우 사인 함수의 값 사용, 홀수인 경우 코사인 함수의 값 사용
- $d_{model}$: 트랜스포머의 모든 층의 출력 차원을 의미하는 하이퍼파라미터
(위의 예시에선 4차원으로 표현되어있으나 실제 논문에서는 512의 값을 가진다.)
이렇게 임베딩 벡터에 포지셔널 인코딩의 값을 더해줌으로써 같은 단어라 해도 문장 내의 위치가 다르니 트랜스포머의 입력으로 들어가게 될 임베딩 벡터의 값이 달라진다. 이제 이 순서 정보가 고려된 임베딩 벡터가 인코더의 Attention 과정을 거치게 된다.
어텐션(Attention)

트랜스포머에서는 총 세 가지의 Attention이 사용되는데 각 Attention은 사용되는 위치에 따라서 하는 일이 다르다.

Self Attention은 본질적으로 Query, Key, Value 가 동일한 경우를 말한다. (이는 세 벡터의 출처가 같다는 것을 의미한다.) 따라서 Encoder - Decoder Attention의 경우 Query가 디코더의 벡터인 반면에 Key와 Value는 인코더에서 받아오는 벡터라 Self Attention이라 부르지 않는다.
인코더(Encoder)

인코더의 구조를 보자.
num_layers는 인코더 층의 개수를 의미하는 하이퍼파라미터로 논문에서는 6개의 인코더 층을 사용하였다. 인코더를 하나의 층이라는 개념으로 생각한다면, 하나의 인코더 층은 크게 총 2개의 서브층(Sublayer)로 나눠진다고 생각해볼 수 있다.
1.Sublayer: Multi-head Self - Attention
: 셀프 어텐션을 병렬적으로 사용한다는 의미
2.Sublayer: Position-wise FFNN
: 일반적인 피드 포워드 신경망
Self - Attention의 동작 원리
1). Query, Key, Value 벡터 얻기
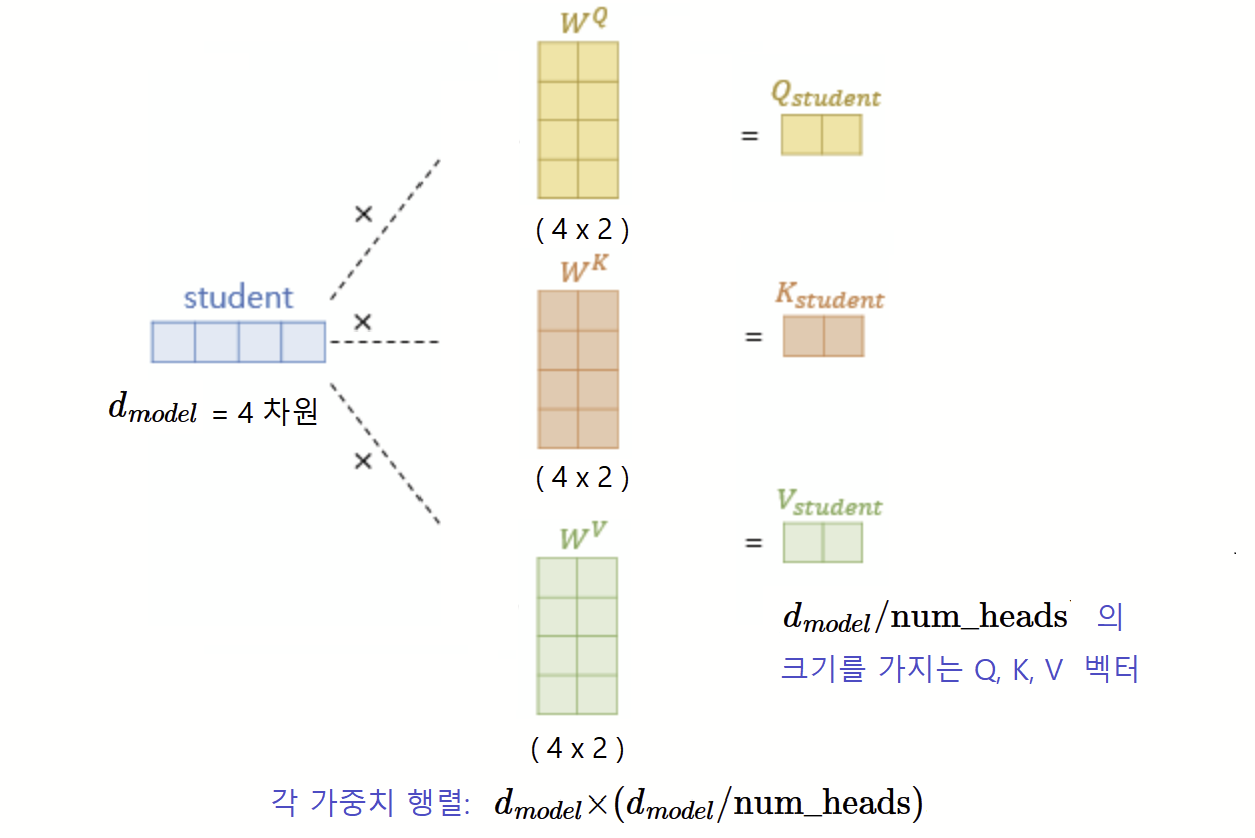
어텐션을 수행하기 위해 입력 문장의 임베딩된 단어 벡터들로부터 위와 같은 과정을 거쳐 Q벡터, K벡터, V벡터를 얻는다. 이때 Q, K, V 벡터는 $d_{model}$ / $num$_$heads$의 차원을 가지는데 논문에서는 $d_{model} = 512$ 의 차원을 가졌던 각 단어 벡터들을 8개로 Head 개수를 정해, $512/8 = 64$의 차원을 가지는 Q, K, V 벡터로 변환하였다. (Head의 개수는 하이퍼파라미터다.) 이때 사용되는 가중치 행렬은 $d_{model}$차원의 데이터를 $d_{model}$ / $num$_$heads$ 의 차원을 가진 데이터로 맵핑해야하니 $d_{model} \times (d_{model} /$ $num$_$heads)$의 크기를 가진다.
student 뿐만이 아니라 모든 단어 벡터에 위와 같은 과정을 거쳐 I, am, a , student 각 단어마다 Q, K, V 벡터를 가진다.
2). Scaled Dot - Product Attention

- Q, K, V벡터를 얻었다면 각 Q벡터는 1)번에서 구한 모든 K벡터에 대해 어텐션 스코어(Attention Score)를 구한다.
- Attention Score는 Q벡터와 문장 내 모든 단어들게서 얻은 K벡터와의 내적을 구한 후 Scale Factor로 나눠서 구한다.
- (내적을 구할 수 있게 K 벡터는 전치시킨다.)
- 식으로 표현하면, $score(q,k) = q ∙ k / \sqrt{n}$ 으로 Dot-Product Attention에 값을 스케일링하는 과정을 추가하였다 해서 Scaled Dot-Product Attention이라 한다.
- $d_k = d_{model}$ / $num$_$heads$로 논문에서는 $d_{model} = 512$, $num$_$heads = 8$을 사용해 $\sqrt{d_k} = 8$이다.
- 이 Attention Score는 단어 I 가 단어 I, am, a, student 의 단어들과 얼마나 연관되어 있는지를 나타내는 수치다.
- 그 수치가 전체 중 어느정도를 차지하는지 보기 위해 Softmax 함수를 사용해준다.
- Attention Score에 Softmax 함수를 사용해 어텐션 분포(Attention Distribution)을 구한다.
- 위의 예시에선, 'I'라는 단어가 'I'라는 단어와 40%의 연관성을, 'am'이라는 단어와는 10%의 연관성을 가진다고 보면 된다.
- 각각의 Attention Distribution에 Value 값들을 곱한 후 다 더해 Attention Value를 구한다.
- 위 모든 과정들을 am에 대한 Q벡터, a에 대한 Q벡터, student에 대한 Q벡터에 대해서도 동일하게 진행한다.
사실 굳이 이렇게 각 Q벡터마다 일일이 따로 연산할 필요는 없다!
2.5). 행렬(Matrix) 곱셉 연산을 이용해 한꺼번에 연산하기
위의 모든 과정들은 벡터 연산이 아니라 행렬 연산을 사용하면 일괄 계산이 가능하다.
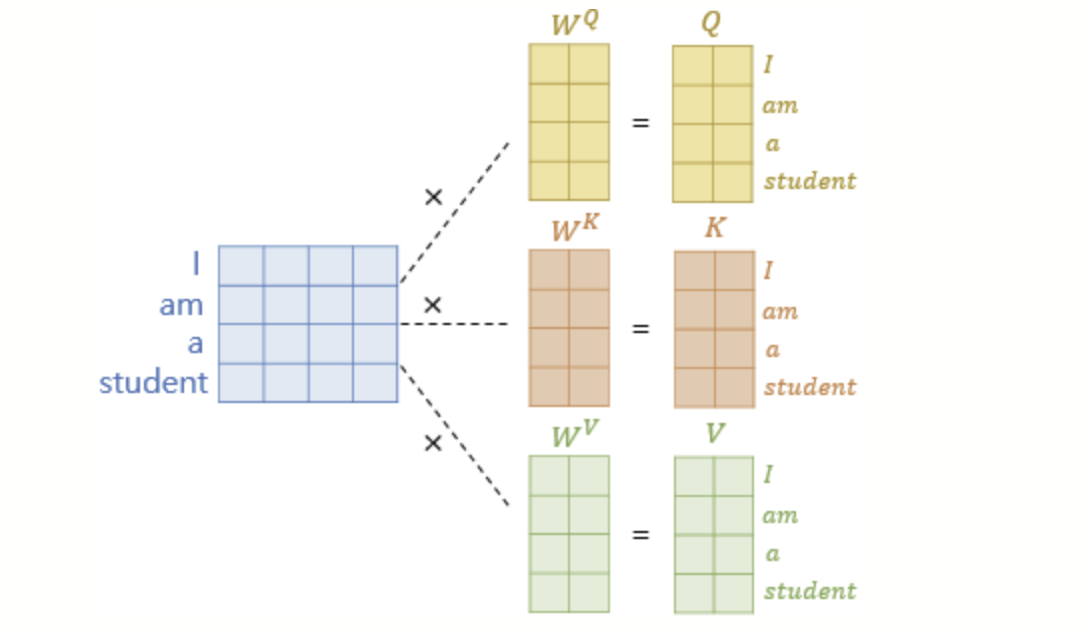
각 단어 벡터마다 일일히 가중치 행렬을 곱하는 것이 아니라 문장 행렬에 가중치 행렬을 곱하여 Q행렬, K행렬, V행렬을 구한다.

Q행렬을 K행렬을 전치한 행렬과 곱해주면, 각각의 단어의 Q벡터와 K벡터의 내적이 각 행렬의 원소가 되는 행렬이 결과로나온다.
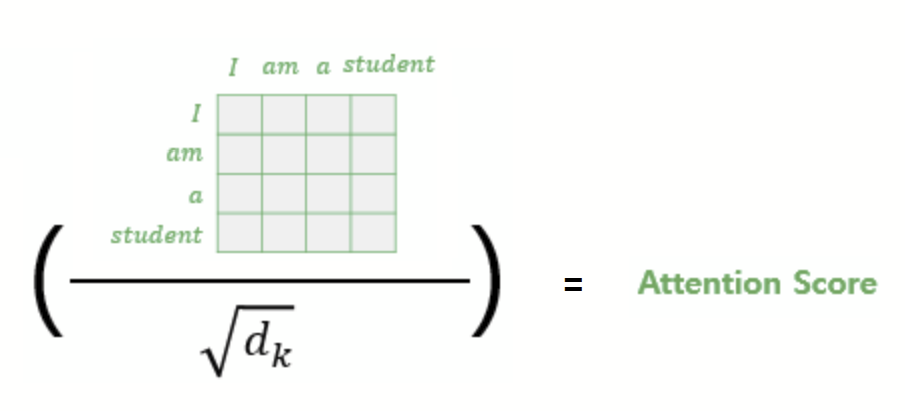
위의 결과 행렬의 값에 전체적으로 $\sqrt{d_k}$를 나누어주면 각 행과 열이 Attention Score 값을 가지는 행렬이 된다.
예로, I 행과 student 열의 값은 I 의 Q 벡터와 student의 K벡터의 어텐션 스코어 값이다. (단어 'I'가 단어 'student'와 얼마나 연관되어 있는가.)
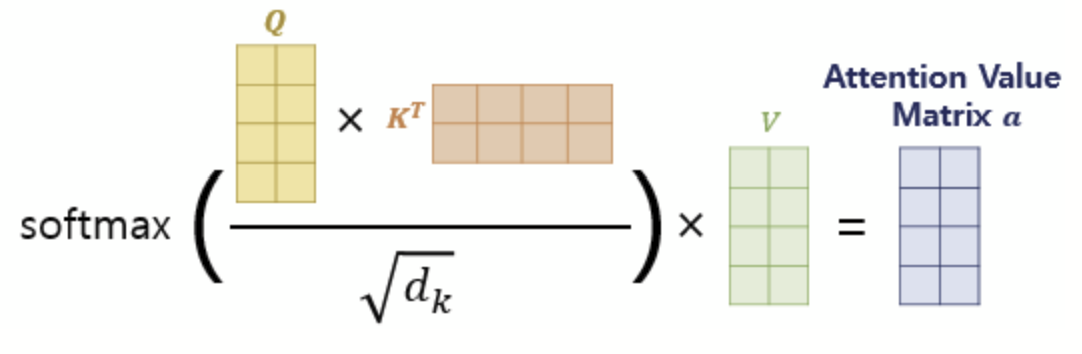
이제 Attention Score 행렬에 Softmax를 취해 Attention Distribution을 구하고 Value 행렬과 곱해 각 단어의 Attention값을 모두 가지는 Attention Value 행렬을 얻는다.

이는 트랜스포머 논문에 기재된 위의 수식으로 표현할 수 있다.
3). Self - Attention의 효과

위의 예시 문장을 번역하면 '그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤하였기 때문이다.' 인데, 여기서 그것(it)에 해당하는 것은 과연 길(street)일까?, 동물(animal)일까? 사람은 피곤한 주체가 동물에 해당한다는 것을 쉽게 알 수 있지만 기계는 그렇지 않다. 하지만 Self Attention은 입력 문장 내의 단어들끼리 유사도(연관성)를 구하므로서 그것(it)이 동물(animal)과 연관되었을 확률이 높다는 것을 찾아낸다.
Multi - Head Attention
1). 병렬 Attention

앞서 말한 Attention에서는 $d_{model}$의 차원을 가진 단어 벡터를 $num_heads$로 나눈 차원을 가지는 Q, K, V 벡터로 바꾼 후 Attention을 수행했다. 왜 $d_{model}$의 차원을 가진 단어 벡터가 아니라 굳이 차원을 축소시킨 벡터로 Attention을 수행하였던 걸까?
Transformer 연구진은 한 번의 Attention 보다 여러번의 Attention을 병렬로 수행하는 것이 더 효과적이라 판단하였다. 따라서 $d_{model}$d의 차원을 가진 단어 벡터를 $num$_$heads$로 나눠 $d_{model}$ / $num$_$heads$ 의 차원을 가지는 Q, K, V 벡터에 대해 $num$_$heads$개의 병렬 Attention을 수행하는 것이다. 논문에서는 하이퍼파라미터인 $num$_$head$의 값을 8로 지정하였다. 즉 위에서 설명한 Attention이 8개로 병렬로 이루어지게 되는데, 이때 각각의 Attention Value 행렬을 Attention Head라 부른다. 이때 Attention을 구하기 위해 사용된 가중치 행렬 $W^Q, W^K, W^V$의 값은 8개의 Attention Head 마다 전부 다르다.

병렬 Attention을 모두 수행하였다면 모든 Attention Head를 연결(concatenate)한다. 모두 연결된 어텐션 헤드 행렬의 크기는 입력 문장의 행렬과 같은 (seq_len, $d_{model}$)가 된다. (위는 head의 연결을 그림으로 표현하기 위해 $d_{model}$의 크기를 $d_v$의 8(Head 개수)인 16차원으로 표현하였으나 실제 Attention Head 들끼리 연결된 위의 행렬은 입력 문장의 차원과 같은 4차원($d_{model}$)의 크기를 가진다.
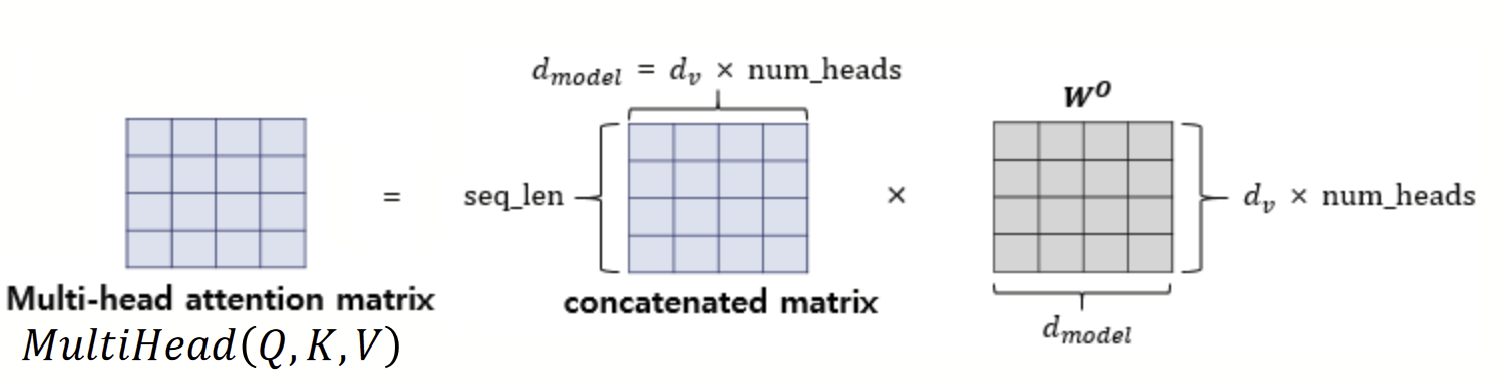
8개의 Attention Head를 모두 연결한 행렬에 또 다른 가중치 행렬 $W^O$을 곱하게 되는데, 이렇게 나온 결과 행렬이 Multi - Head Attention 의 최종 결과물이 된다. 이때 결과물인 Multi - Head Attention 행렬은 인코더의 입력이었던 문장 행렬의 크기와 동일하다.
다시 말해 인코더의 첫번째 서브층인 Multi - Head Attention 단계를 끝마쳤을 때, 인코더의 입력으로 들어왔던 행렬의 크기가 유지되는 것이다.이 행렬의 크기는 다음 서브층인 포지션 와이즈 피드 포워드 신경망에서도 유지되며 인코더의 최종 출력에서도 크기는 동일하게 유지되며, 따라서 그 다음 인코더에서도 다시 입력될 수 있다. (논문에서는 총 6개의 인코더 사용)
2). 병렬 Attention의 효과
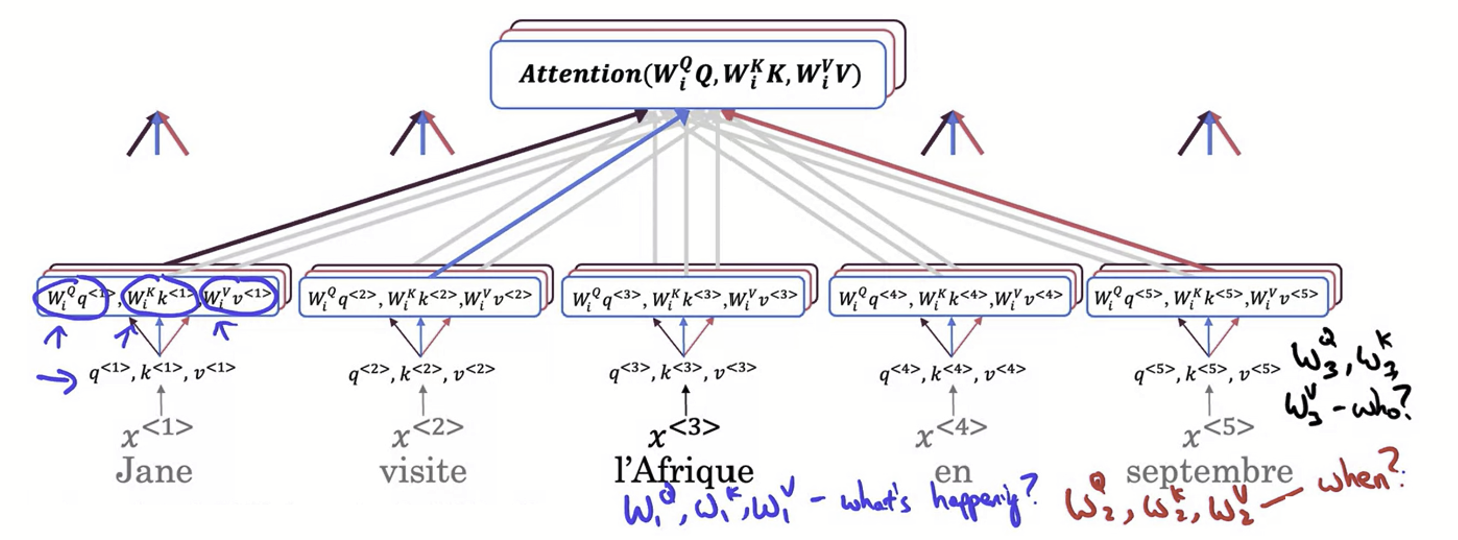
벙렬 Attention으로 얻을 수 있는 효과는 무엇일까? 위와 같은 프랑스 문장을 영어로 번역해야한다고 해보자. 위의 예시에선 총 3개의 Attention이 진행되었다. 이때 문장의 l'Afrique(아프리카) 라는 단어가 Query 라고 하였을때, 이 Query는 Attention 마다 다른 시각으로 문장을 살펴본다.
직관성을 위해 예시로 첫 번째 Attention에서 Query가 l'Afrique 라는 단어에 무슨일이 있었던 것인가? 라는 질문이라고 해보자. 그렇다면 문장 중 'visite'이라는 단어가 해당 질문에 가장 올바른 답이니 l'Afrique 와 visite 사이의 Attention Score 값이 가장 클 것이다.두 번째 Attention에선 Query가 l'Afrique 단어가 언제 일어났던 일인가? 라는 질문이었다고 하면 단어 'septembre'와의 연관도가 가장 높게 나올 것이다. 이렇게 전부 다른 시각에서 얻은 Attention Head를 서로 다른 특징(Feature)라 생각하면 된다. 따라서 구분된 여러 개의 병렬 Attention 수행을 통해 신경망은 문장의 매우 풍부한 표현을 계산할 수가 있다.
포지션 - 와이즈 피드 포워드 신경망(Position-wise FFNN)

포지션 - 와이즈 FFNN 은 인코더와 디코더에 공통적으로 있는 서브층이다. 포지션 - 와이즈 FFNN은 쉽게 말하면 완전 연결 FFNN(Fully-connected FFNN)이라고 해석할 수 있다. 위는 포지션 - 와이즈 FFNN의 수식과 이를 그림으로 표현한 것이다.
$x$는 앞서 Multi - Head Attention의 결과인 (seq_len, $d_{model}$)크기를 가지는 행렬이다. 이때 가중치 행렬 $W_1$은 ($d_{model}, d_{ff}$) 의 크기를, 가중치 행렬 $W_2$은 ($d_{ff},d_{model}$) 의 크기를 가진다. (은닉층의 크기인 $d_{ff}$는 논문에서 2,048의 크기를 가진다.)
*매개변수 $W_1,b_1,W_2,b_2$는 하나이 인코더 층 안에서는 다른 문장, 다른 단어들마다 동일한 값을 가지지만 인코더 층마다는 다른 값을 가진다.*
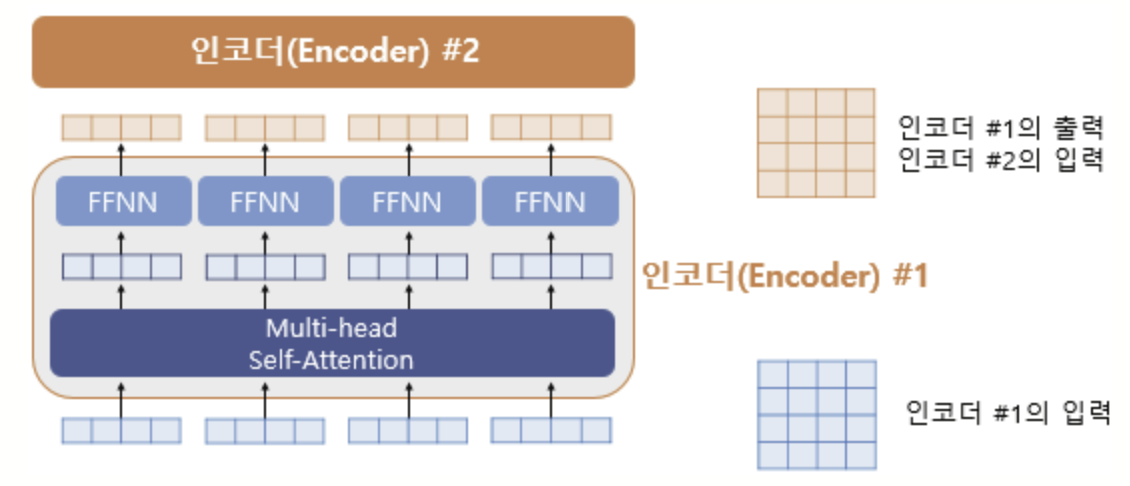
그림 속 좌측은 인코더의 입력을 벡터 단위로 봤을 때, 각 벡터들이 멀티 헤드 어텐션 층이라는 인코더 내 첫번째 서브 층을 지나 두 번째 서브층인 FFNN을 통과하는 것을 보여준다. (실제로는 우측과 같이 행렬로 연산) 인코더의 입력크기 (seq_len, $d_{model}$)는 항상 보존된다.
잔차 연결(Residual connection)과 층 정규화(Layer Normalization)

Transformer에서는 서브층 외에 추가적으로 사용되는 기법이 있는데, 위에 그림 속에 적힌 Add & Norm 으로 잔차 연결(Residual connection)과 층 정규화(Layer normalization)를 의미한다. 추가된 화살표들이 서브층 이전의 입력에서 시작되어 서브층의 출력 부분을 향하고 있는 것에 주목하자.
1) . 잔차 연결(Residual connection)

위 그림은 입력 $x$와 $x$에 대한 어떤 함수 $F(x)$의 값을 더한 함수$H(x)$ 의 구조를 보여준다. 어떤 함수 $F(x)$는 Transformer에선 FFNN이나 Multi - Head Attention 등의 서브층에 해당된다. 즉 잔차 연결은 서브층의 입력과 출력을 더하는 것이라 볼 수 있다. (서브층의 입출력의 행렬이 동일한 차원을 가지니 덧셈 연산이 가능하다.)
잔차 연결은 컴퓨터 비전 분야에서 주로 사용되는 모델의 학습을 돕는 기법이다.

Transformer 안에서의 잔차 연결 예시다. 사용된 서브층은 Multi - Head Attention이다.
2) . 층 정규화(Layer Normalization)

잔차 연결을 거친 결과는 이어서 층 정규화 과정을 거치게 된다. 층 정규화는 텐서의 마지막 차원에 대해서 평균($\mu$)과 분산($\sigma ^2$)을 구하고, 이를 가지고 어떤 수식을 통해 값을 정규화하여 학습을 돕는다.
인코더에서 디코더로
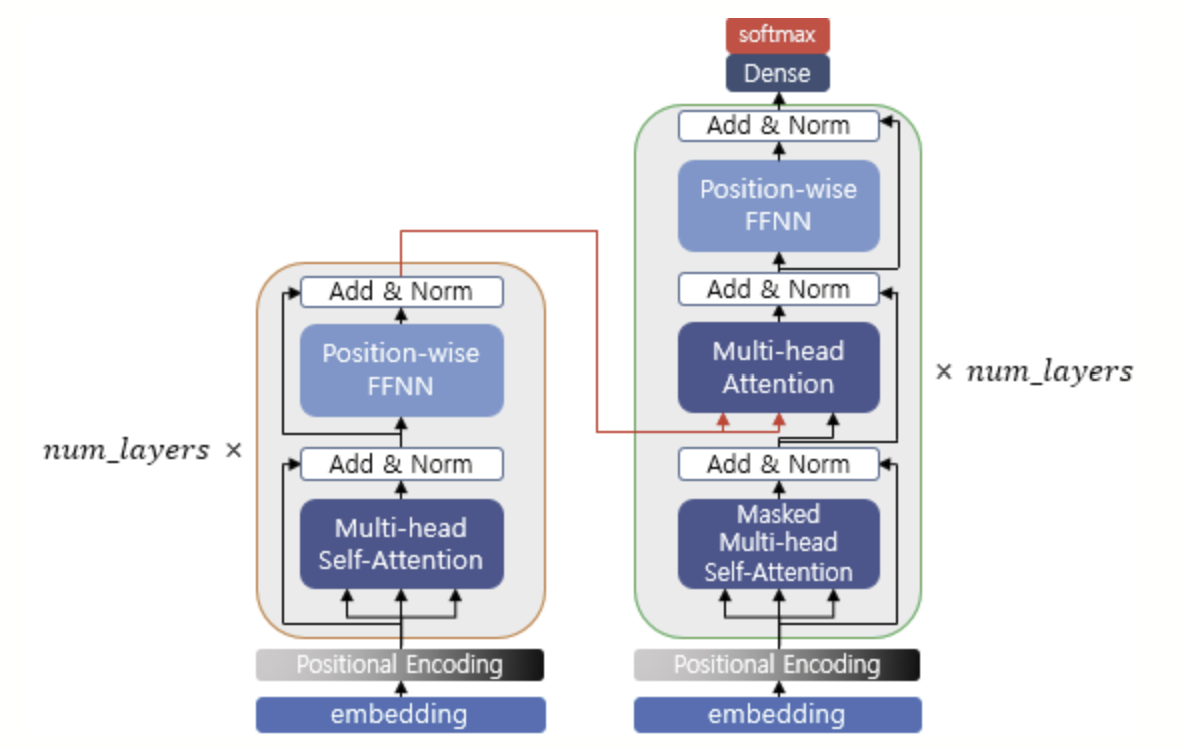
지금까지 인코더에 대해서 알아보았다. 이렇게 구현된 인코더는 총 num_layers만큼의 층 연산을 순차적으로 한 후에 마지막 층의 인코더의 출력을 디코더에게 전달한다. 인코더 연산이 끝났으면 디코더 연산이 시작되어 디코더 또한 num_layers만큼의 연산을 하는데, 이때마다 인코더가 보낸 출력을 각 디코더 층 연산에 사용한다.
디코더의 첫번째 서브층 : Self - Attention과 Look-Ahead Mask
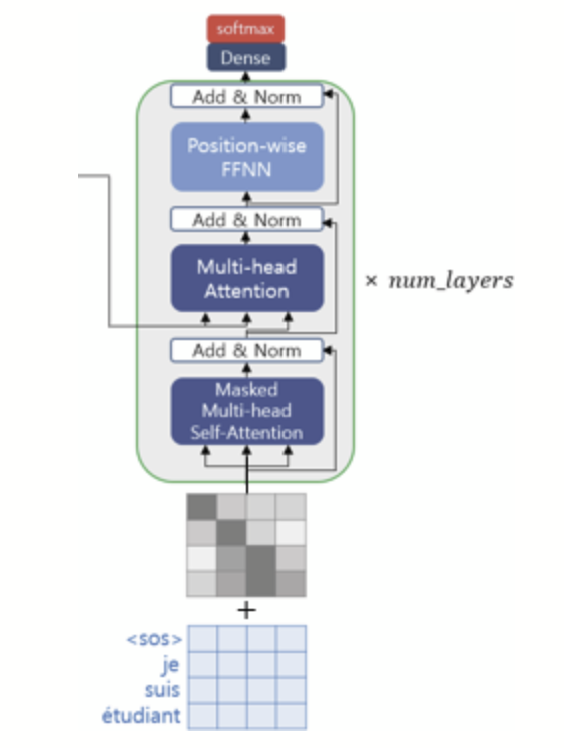
디코더도 인코더와 동일하게 임베딩 층과 포지셔널 인코딩을 거친 후의 문장 행렬이 입력된다. Transformer 또한 seq2seq와 마찬가지로 교사 강요(Teacher Forcing)를 사용하여 훈련되므로 학습 과정에서 디코더는 번역할 문장에 해당되는 <sos> je suis étudiant의 문장 행렬을 한 번에 입력받는다. 그리고 디코더는 이 문장 행렬로부터 각 시점의 단어를 예측하도록 훈련된다.
이때 문제가 생긴다. seq2seq의 디코더에 사용되는 RNN 계열의 신경망은 입력 단어를 매 시점마다 순차적으로 입력받으니 다음 단어 예측에 현재 시점을 포함한 이전 시점에 입력된 단어들만 참고할 수 있다. 반면, Transformer는 문장 행렬로 입력을 한 번에 받으므로 현재 시점의 단어를 예측하고자 할 때, 입력 문장 행렬로부터 미래 시점의 단어까지도 참고할 수 있는 현상이 발생한다.
가령, suis를 예측해야 하는 시점이라고 해보면, RNN 계열의 seq2seq의 디코더라면 현재까지 디코더에 입력된 단어는 <sos>와 je뿐이겠지만, Transformer는 이미 문장 행렬로 <sos> je suis étudiant를 입력받았다.

룩-어헤드 마스크(look-ahead mask)는 디코더의 첫 번째 서브층에서 이루어진다. 디코더의 첫 번째 서브층인 Multi - Head Attention 층은 인코더의 첫 번째 서브층인 Multi - Head Attention 층과 동일한 연산을 수행한다. 오직 다른 점은 Attention Score 행렬에서 마스킹을 적용한다는 점이다.
- 우선 위과 같이 Self - Attention을 통해 Attention Score 행렬을 얻는다.
- 이제 각각의 단어가 자신보다 미래에 있는 단어들은 참고하지 못하도록 마스킹한다.
- (즉 앞쪽에 등장했던 단어들만 참고할 수 있도록 만드는 것이다.)
- 마스킹을 하는 방법: Attention Score 행렬의 마스킹 위치에 매우 작은 음수값을 넣어준다.
- 마스킹 위치엔 매우 작은 음수 값이 들어가 있으므로 Attention Score 행렬이 Softmax 함수를 지나면 해당 위치의 값은 0이 되어 해당 단어와의 연관성은 반영되지 않게 된다.
디코더의 두번째 서브층 : Encoder - Decoder Attention
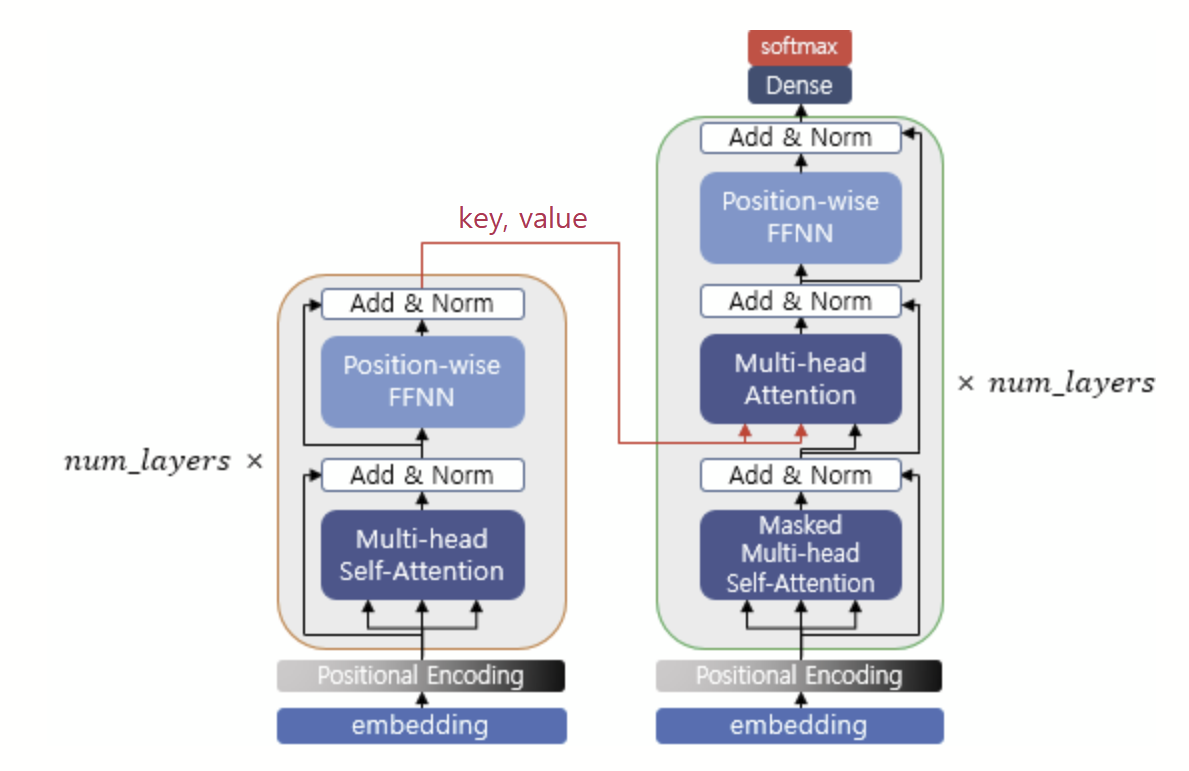
디코더의 두 번째 서브층은 Multi - Head Attention을 수행한다는 점에서는 이전의 어텐션들(인코더와 디코더의 첫번째 서브층)과는 공통점이 있으나 Self - Attention이 아니다. Encoder - Decoder Attention은 Query가 Decoder의 첫 번째 서브층의 결과 행렬로 부터 얻지만, Key와 Value는 Encoder 의 마지막 층에서 온 행렬로부터 얻기 때문이다.

Query가 디코더 행렬, Key가 인코더 행렬일 때, 어텐션 스코어 행렬을 구하는 과정은 위와 같다. 그 외에 Multi - Head Attention을 수행하는 과정은 다른 어텐션들과 같다. 요약하자면, Encoder - Decoder Attention은 출력 단어들이 입력 단어들 중에서 어떤 정보에 더욱더 많은 가중치를 두는지를 구하는 것이라고 볼 수 있다.

위의 예시는 영어문장을 프랑스어로 번역했을 때의 Attention을 나타낸 heat map이다. 이를 통해 각 출력이 어떤 입력 정보를 많이 참고했는지 알 수 있다. (위 예시에서는 색이 밝을 수록 연관성이 높다)
참고
동빈나 - Youtube 'Transformer 논문리뷰'
coursera 강의 'Transformer Network'
wikidocs '16 - 01 트랜스포머(Transformer)'
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| 배치 정규화(Batch Normalization) (0) | 2023.05.20 |
|---|---|
| Feature Scaling (ft. 입력 특성 정규화하기) (0) | 2023.05.19 |
| 최적화 알고리즘 (ft. Momentum, RMSprop, Adam) (1) | 2023.05.18 |
| 지수 가중 평균(Exponentially weighted averages) (0) | 2023.05.17 |
| 경사하강법의 세 종류(BGD, SGD, MGD) (1) | 2023.05.17 |



