경사하강법(Gradient Descent Algorithm)

경사 하강법은 최적화 알고리즘 중 하나로, 손실 함수(Loss Function)의 값을 최소화하는 파라미터[가중치(weight)와 편향(bias)]를 구하기 위해 손실함수에 대한 각 매개변수의 기울기(Gradient)를 이용하는 방법이다.
이 때 기울기가 0인 지점인 손실함수의 값이 최저인 곳이므로 그 지점에 도달하기위해 매개변수는 기울기의 반대방향으로 움직여야 한다. 그래서 경사하강법에서 미분값의 -만큼 빼주는 값으로 가중치를 업데이트하는 것이다.
위에선 예시로 가중치에 대해서만 얘기했으나 다른 매개변수인 편향(Bias)에 대해서도 동일하게 적용된다.
결국 최적해에 도달할때까지 매개변수 업데이트를 반복(Iteration)하는 것인데 하나의 반복에서의 변화식은 같다.
Gradient Descent Algorithm
$w=w−α* \frac{d}{dw}*J(w,b) $
$b=b−α* \frac{d}{db}*J(w,b) $ $α$ : learning rate
이때 경사하강법은 하나의 반복 안에서 다룰 데이터 세트의 크기에 따라 세 종류로 나뉜다.

1. 배치 경사 하강법 (Batch Gradient Descent Method, BGD)

배치 경사 하강법은 보통 경사하강법으로 얘기하며 각 반복마다 모든 훈련 데이터 세트를 처리하는 방법이다. 즉 1 Iteration 안에서 전체 데이터 샘플의 기울기를 계산해한다. 기울기 계산 후 모든 매개변수에 대한 업데이트를 진행한 후 다시 최적의 해에 도달할 때까지 모든 데이터를 가지고 같은 계산을 반복한다. 따라서 수렴하는데 오랜 시간이 걸린다.
2. 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)

확률적 경사 하강법은 첫 단계로 일단 전체 훈련 데이터 세트를 무작위화 한 다음에, 하나의 Iteration 안에서 하나의 테이터에 대해서만 손실함수에 대한 기울기를 계산하여 업데이트를 진행하는 방법이다. 첫 매개변수를 업데이트 하면 그 다음 매개변수를, 또 그 다음인 세 번째부터 마지막 m 번째 데이터까지 기울기 계산 후 업데이트해준다. 물론 마찬가지로 최적의 매개변수 값에 도달할때까지 해당 계산을 반복한다.
3. 미니배치 경사 하강법 (Mini Batch Gradient Descen, MGD)

배치 경사 하강법과 확률적 경사 하강법보다 더 빠르게 작동하는 경사 하강법으로, 전체 훈련 데이터 세트를 여러 작은 그룹(Mini Batch)들로 나눠서 경사 하강법을 진행한다. 하나의 Iteration 안에서 하나의 미니 배치에 속해 있는 데이터들에 대하여 기울기를 구한 후 , 그것의 평균 기울기를 통해 매개변수를 업데이트하는 방식이다.
[위의 식에서 b = 하나의 소그룹(Mini Batch)에 속하는 데이터 수]

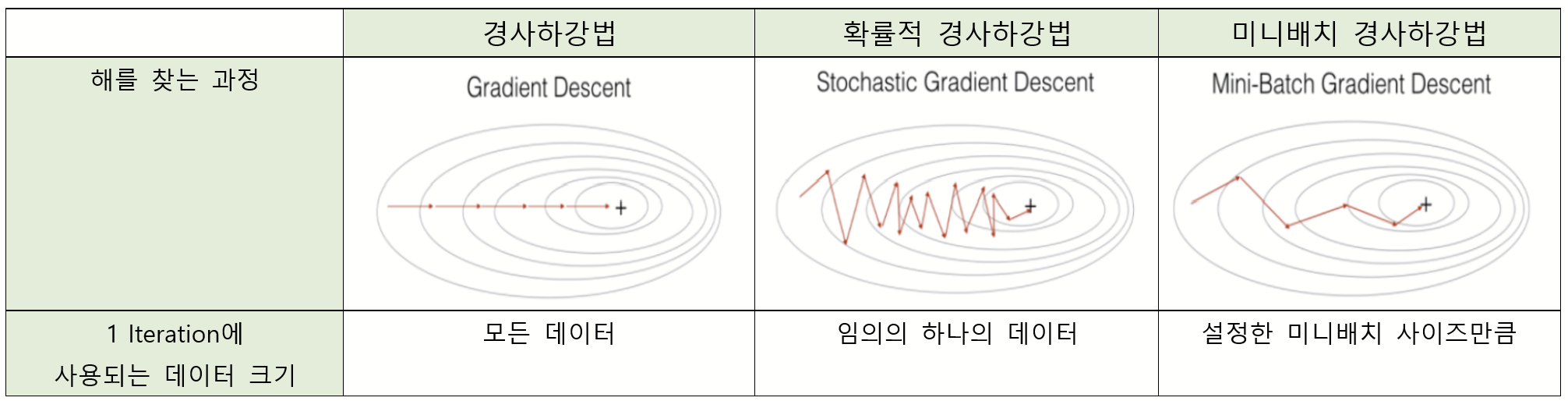
이런 느낌이라고 보면 된다. 하나의 Iteration 에서 BDG는 전체 데이터 세트를, SGD는 임의의 하나의 데이터를, MGD는 설정한 미니 배치 사이즈만큼을 사용한다.
따라서 아래처럼 ↓ 얘기할 수 있다.
전체 데이터 세트 : m 개 일때,
Batch Gradient Descent ➱ Mini-batch size = m
Stochastic Gradient Descent ➱ Mini-batch size = 1
Mini-batch Gradient Descent ➱ Mini-batch size = 1 < n < m
특징
1. 배치 경사하강법(Batch Gradient Descent)
장점
- 하나의 데이터 값이 아닌 모든 훈련 데이터 세트의 평균을 계산하여 매개변수를 업데이트하기 때문에 손실 함수의 전역 최솟값을 향한 노이즈가 별로 없다.
- 벡터화의 이점을 누릴 수 있다.
단점
- Local optimal에 빠질 수 있으나 잡음이 별로 없어 locap optimal 에서 벗어나기가 힘들다.
- 한번의 학습에 모든 데이터 세트를 사용하니 학습이 오래 걸린다.
2. 확률적 경사하강법(Stochastic Gradient Descent)
장점
- 한 번의 학습에 하나의 데이터만 처리되므로 계산 속도가 빠르다.
- 데이터 세트가 더 크다면, 그만큼 매개변수를 더 자주 업데이트하게 되므로 더 빠르게 수렴할 수 있다.
- 빈번한 업데이트로 생긴 잡음(노이즈) 덕에 local optimal 에서 벗어날 수 있다.
단점
- 빈번한 업데이트로 인해 비교적 노이즈가 심하다.
- 노이즈가 많아 손실함수의 최소값으로 수렴하는데 더 오래 걸릴 수 있다.
- 대부분의 경우 전역 최솟값으로 가게 되지만 간혹 잘못된 방향으로 가기도 한다. (Optimal을 찾지 못할 가능성도 있다는 것.)
- 한 번에 하나의 데이터만 다루니 벡터화의 이점을 잃는다.
3. 미니배치 경사하강법(Mini-batch Gradient Descent)
장점
- 빠른 학습 제공
- Local optimal에 갇힌 경우 노이즈를 통해 벗어날 수 있다.
- 벡터화의 이점을 누릴 수 있다.
크기 설정
- 훈련 데이터 세트가 작다면 (m < 2000) 그냥 배치 경사하강법을 사용하자.
- 일반적으로 Batch size는 2의 n승[64,128,256,512]으로 설정한다. (컴퓨터는 2진수로 계산되니까)
참고
https://velog.io/@minjung-s/Optimization-Algorithm
https://www.youtube.com/@Deeplearningai
'인공지능 > Machine & Deep Learning' 카테고리의 다른 글
| 최적화 알고리즘 (ft. Momentum, RMSprop, Adam) (0) | 2023.05.18 |
|---|---|
| 지수 가중 평균(Exponentially weighted averages) (0) | 2023.05.17 |
| 가중치 규제 (Weight Regularization) ft. 과적합 해결하기 (0) | 2023.05.09 |
| Linear Regression 과 Logistic Regression (0) | 2023.05.09 |
| Classification: 붓꽃(Iris) 데이터 분석하기 (1) | 2023.04.19 |